В задачах 115 ¸ 117 вычислить заданный криволинейный интеграл.

один виток винтовой линии от точки А (1;0;0) до точки В (1;0;4p).

116. вдоль дуги кубической параболы 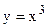от точки А (1;1) до В (2;8).

117. окружность, образованная пересечением поверхностей

118. Найти массу дуги кривой от точки А с абсциссой х = 1 до В с абсциссой
х = 2, если плотность дуги .

119. от .

120. до .

121. .

122. .

123. .

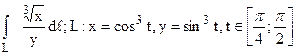124. .

125. .

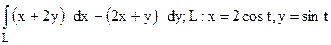
126. от А (–2;0) до В (2;0).

127. от А(0;–1) до В(1;–2).

128. .

В задачах 129 ¸ 138 вычислить поверхностный интеграл. Сделать чертеж поверхности.

129. где – часть поверхности z = 12 – 3x – 4y, ограниченная координатными плоскостями.

130. ограниченная координат-

ными плоскостями . (При вычислении двойного интеграла перейти к полярным координатам).

131.

ограниченная поверхностями y = x, x = 0 и z = 0.

132. лежащая между поверхностями х = 0, z = 0 и у = 1 (у ³ 1). (При вычислении двойного интеграла перейти к полярным координатам)

133. 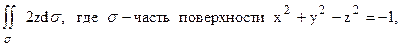ограниченная поверхностью (При вычислении двойного интеграла перейти к полярным координатам).

134. верхняя сторона части поверхности x + y + z = 1, ограниченной координатными плоскостями.

135. поверхности . При вычислении двойных интегралов перейти к полярным координатам.

136. – часть поверхности ограниченная поверхностями . Нормаль к поверхности образует острый угол с осью 0х.

137. внешняя сторона части поверхности ограниченной поверхностями x = 0, y = 0 и z = 1 (x ³ 0,y ³ 0). (При вычислении двойного интеграла по области перейти к полярным координатам).

138. , где – верхняя сторона части поверхности , ограниченной поверхностями х=0, у=0 и х+у=1.

В задачах 139 ¸ 312 вычислить данные криволинейные интегралы.

139. 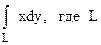– контур треугольника, образованного осями координат и прямой в положительном направлении.

140. 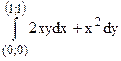вдоль кривой

141. , где L – контур прямоугольника, образованного прямыми
х = 1, х = 3, у = 1, у = 5 в положительном направлении.

142. , где L – четверть окружности x = r cos t, y=r sin t от t=0 до

143. вдоль прямой, соединяющей точки (–1;2) и (2;3).

144. вдоль прямой, соединяющей точки (2;1) и (1;2).

145.

146. 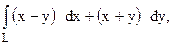где L – отрезок прямой, соединяющей точки А (2;3) и В (3;5).

147. где L – дуга параболы от точки О (0;0) до точки А (2;2).

148.

149.

150.

151. (в первом квадранте).

152. .

153. (в первом квадранте).

154.

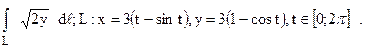
155.

156. .

157. .

158. 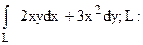дуга кривой от (0;0) до (1;1).

159. .

160. отрезок прямой от (0;0) до (1;3).

161. 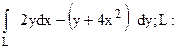дуга кривой проходимая по часовой стрелке.

162. до (1;е).

163. .

164.

165. .

166. прямая от (1;3) до (2;5).

167. в положительном направлении. Использовать формулу Грина – Римана.

168. .

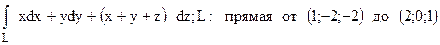169. в положительном направлении. Использовать формулу Грина – Римана.

170. контур треугольника АВС, где А (0;0),

В (1;0), С (1;1). Использовать формулу Грина – Римана.

171. прямая от (1;3) до (4;5).

172.

Использовать формулу Грина – Римана.

173. от (1;1) до (2;2).

174. (предварительно убедиться, что он не зависит от пути интегрирования).

175. отрезок прямой от (1;1;1) до (3;2;4).

176. (предварительно убедиться, что он не зависит от пути интегрирования).

177. (предварительно убедиться, что он не зависит от пути интегрирования).

178. (предварительно убедиться, что он не зависит от пути интегрирования).

179. (предварительно убедиться, что он не зависит от пути интегрирования).

180. 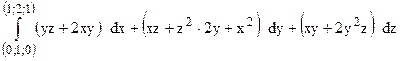(предварительно убедиться, что он не зависит от пути интегрирования).

181. (предварительно убедиться, что он не зависит от пути интегрирования).

182. правый лепесток лемнискаты .

183.

184. .

185. .

186. 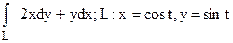(в первом квадранте).

187. .

188. (в первом квадранте).

189. .

190. .

191.

192.

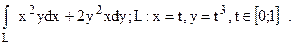
193.

194. дуга кривой у=х² от А (0;0) до В (1;3).

195.

196. прямая от (0;0) до (1;1).

197. при у ³ 0 (по часовой стрелке).

198. от (0;1) до (1; ).

199. (в первом квадранте).

200. .

201.

202.

203. прямая от (0;0) до (p;p).

204. прямая от (1;3) до (2;5).

205. . (По формуле Грина – Римана).

206. прямая от (1;1;1) до (2;3;4).

207. контур треугольника АВС, где А (0;0), В (2;0), С (2,2); по формуле Грина – Римана.

208. по формуле Грина – Римана.

209. прямая от (1;3) до (4;5).

210.

211. от (0;0) до (1;1).

212. 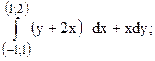предварительно убедиться, что он не зависит от пути интегрирования.

213. предварительно убедиться, что он не зависит от пути интегрирования.

214. предварительно убедиться, что он не зависит от пути интегрирования.

215. предварительно убедиться, что он не зависит от пути интегрирования.

216. предварительно убедиться, что он не зависит от пути интегрирования.

217. предварительно убедиться, что он не зависит от пути интегрирования.

218. предварительно убедиться, что он не зависит от пути интегрирования.

219. предварительно убедиться, что он не зависит от пути интегрирования.

220.

221.

222. в первом квадранте.

223. .

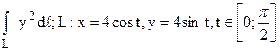224. в первом квадранте.

225. .

226. .

227. .

228. .

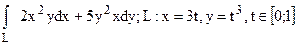229.

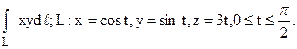
230. .

231.

232. прямая от (0;0) до (1;2).

233. по часовой стрелке.

234. от (0;1) до (1;е).

235. 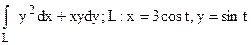в первом квадранте.

236. .

237.

238. .

239.

240. прямая от (0;0) до (p;2p).

241. прямая от (1;3) до (2;5).

242. по формуле Грина – Римана.

243. прямая от (2;2;2) до (2;4;5).

244. по формуле Грина – Римана.

245. контур треугольника АВС, где А (0;0), В (1;0), С (1;1); по формуле Грина – Римана.

246. прямая от (1;3) до (4;5).

247. по формуле Грина – Римана.

248. .

249. 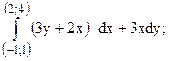предварительно убедиться, что он не зависит от пути интегрирования.

250. предварительно убедиться, что он не зависит от пути интегрирования.

251. предварительно убедиться, что он не

зависит от пути интегрирования.

252. 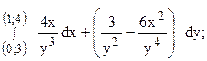предварительно убедиться, что он не зависит от пути интегрирования.

253. 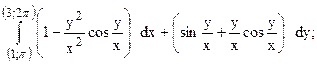предварительно убедиться, что он не зависит от пути интегрирования.

254. предварительно убедиться, что он не зависит от пути интегрирования.

255. предварительно убедиться, что он не зависит от пути интегрирования.

256. предварительно убедиться, что он не зависит от пути интегрирования.

257.

258.

259. в первом квадранте.

260. .

261. в первом квадранте.

262. .

263. .

264.

265. .

266. .

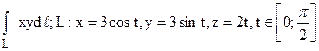267. 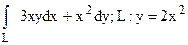от (0;0) до (1;2).

268. 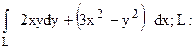прямая от (0;0) до (1;3).

269. при у ³ 0, по часовой стрелке.

270. от (0;1) до (1; ).

271. в первом квадранте.

272. .

273.

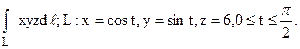
274. .

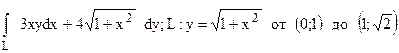275. прямая от (0;0) до (p;p).

276. прямая от (1;3) до (2;5).

277. по формуле Грина – Римана.

278. прямая от (1;–1;–1) до (2;1;2).

279. по формуле Грина – Римана.

280. контур треугольника АВС, где А (0;0), В (2;0), С (2;2); по формуле Грина – Римана.

281. 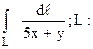прямая от (1;3) до (4;5).

282.

283. от (1;1) до (2;2).

284. предварительно убедиться, что он не зависит от пути интегрирования.

285. прямая от (1;1;1) до (3;2;4).

286. предварительно убедиться, что он не зависит от пути интегрирования.

287. предварительно убедиться, что он не зависит от пути интегрирования.

288. предварительно убедиться, что он не зависит от пути интегрирования.

289. предварительно убедиться, что он не зависит от пути интегрирования.

290. предварительно убедиться, что он не зависит от пути интегрирования.

291. предварительно убедиться, что он не зависит от пути интегрирования.

292. предварительно убедиться, что он не зависит от пути интегрирования.

293. 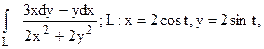в первом квадранте.

294. .

295. .

296. прямая от (0;0) до (1;2).

297. при у ³ 0, по часовой стрелке.

298. от (0;1) до (1;е).

299. в первом квадранте.

300. .

301. прямая от (0;0) до (p;2p).

302. 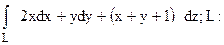прямая от (1;–1;–1) до (2;1;2).

303. по формуле Грина – Римана.

304. контур треугольника АВС, где А(0;0), В(1;0), С (1;1); по формуле Грина – Римана.

305. прямая от (1;3) до (4;5).

306. по формуле Грина.

307. прямая от (1;1;1) до (3;2;4).

308. предварительно убедиться, что он не зависит от пути интегрирования.

309. прямая от (1;1;1) до (3;2;4).

310. предварительно убедиться, что он не зависит от пути интегрирования.

311. предварительно убедиться, что он не зависит от пути интегрирования.

312. 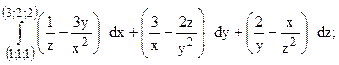предварительно убедиться, что он не зависит от пути интегрирования.

313.

314. Вычислить площадь части поверхности параболоида вырезанной цилиндром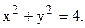

315. отсеченная плоскостью z=1.

316.

Date: 2016-07-22; view: 788; Нарушение авторских прав