Задачи для самостоятельного решения.

1. Вычислить вдоль дуги окружности от точки А(2;0) до точки В().

2. Вычислить вдоль кривой L, заданной уравнением x²-y²=1, от точки А(1;0) до точки В(2; ).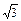

3. Вычислить вдоль кривой x=y²–1 от точки А(-1;0) до точки В(1; ).

4. Вычислить вдоль кривой x=t-sin t, y=1-cos t от точки А(0;0) до точки В(2p;0).

5. Вычислить 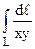вдоль кривой: x=cos³t, y=sin³t;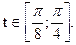

6. Вычислить вдоль кривой y=cosx от точки А(p;-1) до точки В(0;1).

7. Вычислить вдоль кривой y= x; 1 £ x £ e.

8. Вычислить вдоль кривой 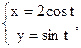от точки А(0;1) до точки В(2;0).

9. Вычислить вдоль кривой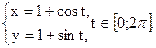

10. Вычислить вдоль кривой y=e^x от точки А(0;1) до точки В(;2).

В задачах 11 41 вычислить криволинейный интеграл по заданной кривой L.

11.

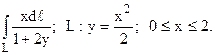
12.

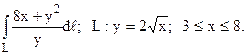
13.

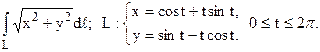
14.

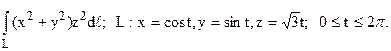
15.

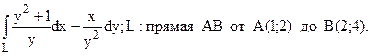
16. 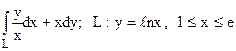от А (1;0) до В (е;1).

17.

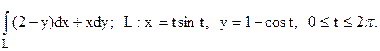
18.

19. Вычислить по формуле Грина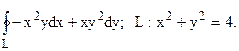

20. Вычислить по формуле Грина L: контур D АВС, пробегаемый в положительном направлении; А(3;-3), В(3;3), С(0;0).

21. точки А(–2;0) до В(1; ).

22.

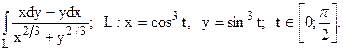
23. от точки А(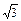;1) до В(0;2).

24. 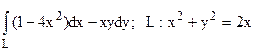от точки А(2;0) до В(1;1).

25. от точки А(1;0) до В(е²;2).

26. от точки А(0;2) до В(3;0).

27. от точки А(2;1) до точки В(0;1).

28. от точки А(1;0) до точки В(e;1).

29.

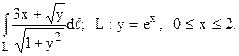
30. от точки А(0;0) до точки В().

31. от x=2 до x=4.

32. первая четверть x²+y²=R².

33. прямая ОА, где О(0;0), А(2;2).

34. от точки O(0;0) до точки A(2;2).

35. 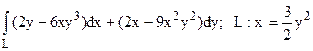от точки O(0;0) до точки A(2;2).

36. от точки O(0;0) до точки A(2;2).

37. прямая АВ, где А(0;0),В(4;3).

38.

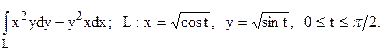
39.

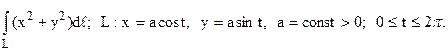
40.

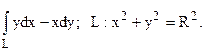
41. отрезок прямой от точки А(1;2) до точки В(3;7).

42. Найти массу материальной линии х=е^у между точками А и В, для которых ординаты равны О и соответственно, если в каждой точке линии АВ плотность распределения массы пропорциональна квадрату абсциссы точки.

43. Вычислить где АВ–часть эллипса 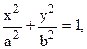лежащая в первой координатной четверти.

44. Вычислить где АВ–часть гиперболической спирали r= от до (r, j–полярные координаты).

45. Вычислить где L–замкнутый контур, состоящий из отрезка ОА полярной оси длиной “а”, дуги АВ окружности r=а и отрезка ВО луча
(r,j–полярные координаты).

В задачах 46 51 вычислить криволинейный интеграл по заданной линии L.

46. L– отрезок прямой от (0;0) до (1;2).

47. L– дуга параболы ОА с вершиной в точке О и осью симметрии Ох, от точки О(0;0) до А(1;2).

48. L– ломаная ОВА, где О(0;0), В( 3),А(1;2).

49. L– отрезок прямой от (0;0) до (1;2).

50. L– дуга параболы ОА с вершиной в точке О и осью симметрии Ох, от точки О(0;0) до А(1;2).

51. L– ломаная ОВА, где О(0;0), В( 3),А(1;2).

52. Найти работу А переменной силы вдоль эллипса от точки В(-2;0) до С (2;0).

53. Вычислить L–линия пересечения поверхности х²+у²=R² c поверхностью z= –1.

В задачах 54 57 вычислить криволинейный интеграл для заданных контуров интегрирования и подинтегральных функций.

54. L:y=2x-x² от точки (1;1) до точки (3;-3); P=y+x²; Q=2x-y.

55. L:y²=9x от точки (0;0) до точки (1;3); P=y², Q=xy-y².

56. L–замкнутая ломаная АВСА, где А(-2;0), В(0;0), С(0;1); P=x(y-2), Q= y(2-x).

57. L:x=e^t, y=e^–t, z=t² (0 £ t £ 1); P=xy, Q=zx², R=xyz.

58. Вычислить где L ограничивает область: 0 < х < 1, 0 < у < х².

59. Вычислить с помощью криволинейного интеграла площадь S_D фигуры D, ограниченной контуром ОАВСО, если О(0;0), А(1;3), В(0;4), С(-1;2); ОА, ВС, СО – отрезки прямых, АВ – дуга параболы у=4–х².

60. Доказать, что значение криволинейного интеграла не зависит от вида линии, соединяющей точки А(-2;-1) и В(3;0), и в случае положительного ответа найти значение данного интеграла.

61.Вычислить криволинейный интеграл 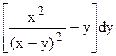как разность значений потенциальной функции в конечной точке (2;0) и начальной точке (0;-1) пути интегрирования.

В задачах 62 64 вычислить с использованием формулы Грина криволинейный интеграл 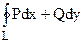для заданных контуров L (пробегаемых в положительном направлении) и подинтегральных функций P и Q.

62. L: ломаная АВСА, где А(1;1), В(2;2), С(1;3); P=2(x²+y²), Q=(x+y)².

63. L: контур, ограничивающий область D в третьей координатной четверти, заданную неравенствами -5 < х+у < -3; Q=x cosy.

64. L: x²+y²=R²; P=–x²y, Q=xy².

В задачах 65 67, убедившись, что выражение Pdx+Qdy является полным дифференциалом, вычислить криволинейный интеграл для заданных точек А и В и функций P и Q.

65.

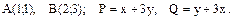
66.

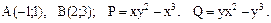
67.

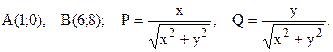
68. Вычислить где S – часть поверхности 2аz=x²+y² (a>0), вырезанная поверхностью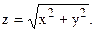

69. Вычислить где S – часть поверхности у=х²–4, отсекаемая плоскостями z=–2y и z=0.

70. Вычислить где L – контур треугольника с вершинами в точках А(1;0), В(0;1), О(0;0).

71. Вычислить где L – верхняя половина эллипса х=а сos t,
y=b sin t, пробегаемая по часовой стрелке.

72. Вычислить поверхностный интеграл где S – поверхность куба
0 £ х £ 1, 0 £ у £ 1, 0 £ z £ 1.

73. Вычислить L: отрезок прямой от D(0;0) до А(1;2).

74. Вычислить 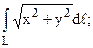L: x²+y²=4x (x ³ 0).

75. Вычислить L: y= от точки А(4;0) до В(0;-2).

76. Вычислить L: x²+y²=4 (x ³ 0, y ³ 0).

77. Вычислить L:2x+y=2 от А(1;0) до В(0;2).

78. Вычислить L:4x+y²=4 от А(1;0) до В(0;2).

79. Вычислить L:=cos t, y=2sin t от А(1;0) до В(0;2).

80. Вычислить L: прямая АВ где А(-1;0) до В(0;1).

81. Вычислить L:x=cos³t, y=sin³t от точки А(-1;0) до В(0;1).

82. Вычислить L:x=t cost, y=t sint, z=t ( ).

83. Вычислить 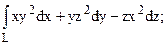L: прямая от точки О(0;0;0) дo
В(-2;4;5).

84.Вычислить 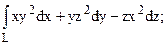L: дуга окружности

от точки А(3;-6;0) до В(-2;4;5).

85. Вычислить L: периметр DАВС, где А(-1;0) до В(0;2), С(2;0).

86. Вычислить L: периметр АВСD, где А(0;0) до В(1;1), С(1;1), D(0;1).

87. Вычислить L: x=cos t, y=sin t.

88. Вычислить L: дуга y=x² от А(-1;1) до В(1;1).

89. Вычислить 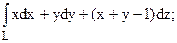L–прямая АВ, где А(1;1;1), В(2;3;4).

90. Вычислить L: y=x от О(0;0) до А(1;1).

91. Вычислить L: y=x² от О(0;0) до А(1;1).

92. Вычислить L: y=2x² от А(2;8) до В(4;32).

93. Вычислить .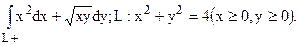

94.Вычислить .

95.Вычислить .

96. Вычислить .

97. Вычислить .

98.Вычислить .

99. Вычислить .

100. Вычислить .

101. Вычислить .

102. Вычислить .

103. Вычислить .

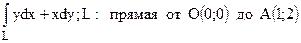104. Вычислить О (0;0) до A (1;2).

105. Вычислить O (0;0), B (1;0), A (1;2).

106. Вычислить 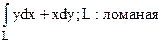OCA, где О (0;0), C (0;2), A (1;2).

107. Вычислить прямая от O (0;0) до A (1;2).

108.Вычислить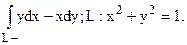

109.Вычислить ABC, где A(1;1), B(2;2), C(1;3).

110.Вычислить .

111. Вычислить

112.

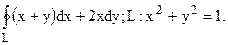
113.

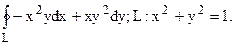
114. Вычислить

Date: 2016-07-22; view: 400; Нарушение авторских прав