Формула Грина и ее применение.

Важную роль в практических приложениях играет теорема, выражающая криволинейный интеграл через двойной по области s, имеющей своим контуром линию L.

Теорема Грина.

Если функции P(x, y) и Q(x, y) непрерывны вместе со своими частными производными ¶Q/¶x и ¶P/¶y в области s, то имеет место формула:

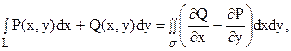
где L – граница замкнутой области s, и интегрирование вдоль L производится в положительном направлении.

Формула Грина имеет место для любой области s, ограниченной кусочно-гладким контуром L. Из (20) следует, что формулу Грина удобно применять для вычисления интегралов второго рода по замкнутому контуру.

Пример 11.

Вычислить интеграл по окружности x² + y² = 2x, пробегаемой против часовой стрелки (рис. 6).

В рассматриваемой задаче . Обе функции непрерывны вместе со своими производными 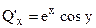на всей плоскости, поэтому

где D – круг, ограниченный данной окружностью (x² – 1)² + y² = 1, т.е. круг радиуса 1 с центром в А(1;0). Вспоминая, что интеграл, стоящий в правой части, есть площадь области, получим: I = 3p.

Пример12.

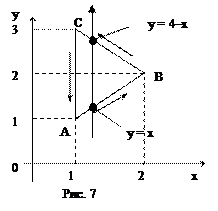Применяя формулу Грина, вычислить где 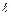– контур треугольника с вершинами в точках А(1;1), В(2;2) и С(1;3) (рис. 7).

В данном случае P = 2(x² + y²),

Применяя формулу Грина, получаем:

Вычисляя двойной интеграл, найдем (рис. 7):

Date: 2016-07-22; view: 1148; Нарушение авторских прав