Формула Остроградского – (Гаусса).

Ранее мы рассмотрели формулу Грина, выражающую связь между двойным интегралом по плоской области и криволинейным интегралом второго рода по контуру этой области.

Теперь мы приведем формулу, устанавливающею связь между поверхностным интегралом второго рода по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью.

Рассмотрим тело Т, ограниченное поверхностью S, обозначим через s_ху проекцию тела Т на плоскость Оху. Пусть, кроме того, в теле Т определена непрерывная функция R(x, y, z), имеющая непрерывную частную производную ¶R(x, y, z)/ ¶z. Тогда существует тройной интеграл который равен поверхностному интегралу от функции R(x, y, z) (интегралу второго рода) по поверхности S, ограничивающей это тело, т. e.

(15)

Легко видеть, что формула (15) верна для любого тела Т, которое можно разбить на конечное число тел. Если допустить, что в теле Т определены еще две непрерывные функции P(x, y, z) и Q(x, y, z), имеющие непрерывные частные производные ¶Р/¶х и ¶Q/¶y, то, при соответствующих предположениях, имеем аналогичные формулы:

Складывая почленно формулы (15), (16) и (17), получим:

поскольку

(см. формулу связи ПИВР и ПИПР).

Формула (18) называется формулой Остроградского-Гаусса.

Она устанавливает связь между тройным интегралом по телу Т и поверхностным интегралом второго рода по внешней стороне поверхности S, ограничивающей тело Т. Заметим, что формула Остроградского остается справедливой для любого тела Т, которое можно разбить на конечное число тел рассмотренного выше вида.

Пример 6.

Вычислить по формуле Остроградского интеграл + (y + 1)dxdz + zdxdy

В нашем случае имеем Р = х, Q = y+1, R = z, и, следовательно,
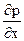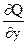+ + = 1 + 1 + 1 = 3. И тогда по формуле Остроградского получаем:

где Т означает тело, ограниченное четырьмя плоскостями: х = 0,
у = 0, z = 0, х + у + z = 1.

Используя правило вычисления тройных интегралов, в декартовых координатах получаем:

Подставив (20) в (19), получим:

Формула Стокса.

Пусть в пространстве имеется гладкая двусторонняя поверхность S, ограниченная замкнутым гладким контуром L (рис. 5).

Обозначим через s_xy проекцию поверхности S на плоскость Oху и будем считать, что поверхность S задана уравнением z = f(x,y), причем, функции
f(х, у), f’_x(x, y), f’_y(x, y) непрерывны в области s_ху, которую будем считать замкнутой и ограниченной.

Выберем на поверхности S определенную сторону, например, верхнюю и установим соответственно, положительное направление обхода контура L по выбранной (верхней) стороне поверхности S, что означает следующее: наблюдатель, следуя вдоль контура L по выбранной (верхней) стороне поверхности S видит эту сторону поверхности слева от себя (или, что то же самое: обход должен ему казаться происходящим против движения часовой стрелки).

Пусть, наконец, на поверхности S и на ее границе L заданы три непрерывные функции P(x, y, z), Q(x, y, z), R(x, y, z) с непрерывными же производными первого порядка.

Тогда имеет место равенство:

Это равенство и называется формулой Стокса.

Оно устанавливает связь между поверхностным интегралом по выбранной стороне поверхности S и криволинейным интегралом по границе L этой поверхности, причем обход по кривой L совершается по тому правилу, которое указано выше.

В иной (условной) записи формула Стокса выглядит так:

где cosa, cosb, cosg – направляющие косинусы нормали к поверхности S, направленной в ту сторону, относительно которой обход контура L совершается против хода часовой стрелки.

Заметим, что формула Стокса имеет место для любой незамкнутой, ограниченной контуром L поверхности S, состоящей из конечного числа поверхностей рассмотренного вида.

Пример 7.

Вычислить по формуле Стокса интеграл

где L – окружность, заданная уравнениями x² + y² = 1,
z = 1, а в качестве поверхности S взят параболоид 2 – z = x² + + y², натянутый на L (рис. 6).

В нашем случае Р = ху, Q = y², R = z, и, следовательно:

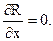
Выбрав на параболоиде верхнюю сторону поверхности и, тем самым, определив направление обхода контура L, получим по формуле Стокса (21):

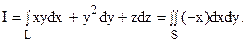
В соответствии с правилом вычисления поверхностных интегралов второго рода будем иметь:

где двойной интеграл вычисляется по кругу s_ху, который является проекцией поверхности S на плоскость Oxy. Последний интеграл разумно вычислять в полярных координатах:

Date: 2016-07-22; view: 525; Нарушение авторских прав