Криволинейные интегралы второго рода (по координатам) – КИВР.

Пусть в пространстве Oxyz задана непрерывная кривая АВ, в точках которой определена произвольная функция P(x, y, z).

Проделаем 5 операций:

1. Разобьем кривую АВ на n частей точками М₀, М₁,…,М_n, следующими друг за другом в направлении от А к В (здесь точки М₀, М_n означают, соответственно, А и В). Координаты точек М_k (k = 1, 2, …, n) обозначим через x_k, y_k, z_k, а наибольшую из длин дуг М_k-1 М_k обозначим через l.

2. На каждой дуге М_k-1 М_k (k = 1, 2, …, n) выберем произвольным образом по точке N_k(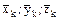) и вычислим в них значения функции
Р(x, y, z), т.е. найдем числа Р().

3. Вычислим произведения Р() (k = 1, 2, …, n), где = x_k – x_k-1.

4. Найдем сумму Р() , которую называют интегральной суммой для функции P(x, y, z) на дуге АВ по переменной х, отвечающей данному дроблению дуги АВ на части и выбору точек N_k ().

5. Измельчая дробление, ищем предел

Если существует конечный предел (8), не зависящий ни от способа дробления кривой АВ на части, ни от выбора точек N_k() (k = 1, 2, …, n), то этот предел называют криволинейным интегралом по переменной х от функции Р(x, y, z) по кривой АВ в направлении от А к В и обозначают символом:

Если на кривой АВ заданы функции Q(x, y, z) и R(x, y, z), то аналогичным образом можно определить криволинейные интегралы по кривой АВ в направлении от А к В по переменным y и z, соответственно, от функций Q(x, y, z) и R(x, y, z):

Сумму криволинейных интегралов (9), (10), (11) называют криволинейным интегралом второго рода по кривой АВ в направлении от А к В и обозначают:

Рассмотрим основные свойства криволинейных интегралов вида (9) (криволинейные интегралы вида (10), (11), (12) обладают аналогичными свойствами), предполагая существующими все ниже встречающиеся интегралы.

1. При изменении направления на кривой криволинейный интеграл второго рода меняет знак на обратный:

2. Постоянный множитель в подынтегральной функции можно выносить за знак криволинейного интеграла:

3. Криволинейный интеграл от суммы двух функций равен сумме интегралов от этих функций:

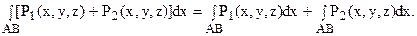
4. Если кривая АВ разбита точкой С на две части АС и СВ, то криволинейный интеграл по всей кривой АВ равен сумме интегралов по ее частям:

5. Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

Криволинейный интеграл по замкнутой кривой L иногда обозначают символом . Направление обхода контура L задается дополнительно. Если L – замкнутая плоская кривая без точек самопересечения, лежащая, например, в плоскости Oxy, то положительным направлением обхода контура L называется такое направление обхода, при котором движение происходит против часовой стрелки, т.е. так, что ограниченная контуром L часть плоскости остается слева (рис. 2). Противоположное направление обхода контура называют отрицательным.

При отсутствии дополнительных указаний о направлении обхода плоского контура L обычно принимают положительное направление.

В заключение общих положений приведем формулу, устанавливающую связь между криволинейными интегралами первого и второго рода.

Пусть АВ – направленная пространственная кривая с началом в точке А и с концом в точке В. Будем касательной, проведенной в любой точке кривой АВ, присваивать направление, совпадающее с направлением кривой АВ. Обозначим через a, b, g углы, которые образует положительное направление касательной в любой точке АВ, соответственно, с осями Ox, Oy, Oz. В этом случае имеют место равенства:

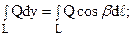
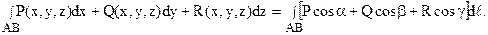
Заметим, что если изменить направление кривой, то не только интеграл слева изменит знак, но и интеграл справа тоже изменит знак, т.к. изменение направления касательной изменит углы a, b, g на + p.

Вычисление криволинейных интегралов второго рода сводится к вычислению определенных интегралов.

Специфика вычисления определяется, как и ранее, способом задания кривой интегрирования.

Пусть кривая АВ задана параметрическими уравнениями

где j(t), y(t), c(t) – непрерывно дифференцируемые функции параметра t. Предположим, что точке А соответствует значение параметра t =a, точке В соответствует
t = b, причем, изменению t от a до b соответствует движение точки М[j(t); y(t); c(t)] по кривой АВ в направлении от А к В. Тогда, если функции
P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны, имеет место формула:

Таким образом, для вычисления криволинейного интеграла второго рода по кривой АВ в направлении от А к В следует: используя параметрические уравнения (14) кривой АВ, заменить под знаком интеграла переменные x, y, z, а также их дифференциалы dx, dy, dz через параметр t, а затем вычислить от полученного выражения определенный интеграл по переменной t в пределах от a доb.

x = j(t), y = y(t), a < t < b,

а функции P(x, y) и Q(x, y) непрерывны на АВ, то формула для вычисления криволинейного интеграла второго рода по кривой АВ имеет вид:

y = f(x), a < x < b,

где f(x) – непрерывно дифференцируемая функция на [a, b], то, принимая х за параметр, как частный случай формулы (17) получим формулу:

где а = х_нач, в = х_кон.

Если различные участки контура заданы различными уравнениями, то нужно разбить контур интегрирования на соответствующие части и весь интеграл вычислять как сумму интегралов, взятых по этим частям.

При работе с интегралом второго рода особо следует помнить, что на линии, по которой он вычисляется, должно быть выбрано одно из двух возможных направлений.

Пример 7.

Вычислить интеграл вдоль линии у= х²/2 от точки А(2;2) до В(0;0) (рис. 3).

Имеем случай явного задания плоской кривой уравнением у = у(х), поэтому данный интеграл второго рода может быть вычислен как определенный интеграл по формуле (19):

где х_нач и х_кон – абсциссы начальной и конечной точек.

Таким образом, имеем:

Пример 8.

Вычислить по верхней половине окружности
x² + (y-1)² = 9, пробегаемой по часовой стрелке.

Из уравнения в декартовых координатах данной линии можно получить ее параметрическое задание более удобное для вычислений: x = 3cost, y = 1 + 3sint, 0 < t < p, причем, начальной точке при заданном условием направлении обхода соответствует t = p, а конечной – t = 0. Здесь удобно использовать формулу (17):

И тогда

Пример 9.

Вычислить – дуга параболы z = x² явное задание кривой, пробегаемая от точки А (-1;1) до точки В (1;1) (рис. 5).

Так как z = x², z’ = 2x и при движении из точки А в точку В х меняется от –1 до 1, то по формуле (19) имеем:

Пример 10.

Вычислить где L – отрезок прямой, соединяющий точки А(1;1;1) и В(2;3;4).

Уравнение прямой, проходящей через две данные точки, имеет вид:

или (так удобнее) x = t + 1, y = 2t + 1, z = 3t + 1.

При передвижении от точки А к точке В параметр t меняется от 0 до 1. По формуле (15) имеем:

Date: 2016-07-22; view: 597; Нарушение авторских прав