Связь между поверхностными интегралами первого и второго рода.

Пусть S – гладкая двусторонняя поверхность, на которой выбрана определенная сторона. Пусть также на поверхности S заданы непрерывные функции P(x, y, z), Q(x, y, z), R(x, y, z). Если написанные ниже интегралы существуют, то поскольку dy dz =cos α ds, dxdz = cos β ds, dxdy = cos γ ds, имеет место формула:

где cosa, cosb, cos g – направляющие косинусы нормали к поверхности S, направленной в выбранную сторону; 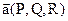– векторная функция, - единичный вектор нормали .

Здесь уместно отметить, что если на поверхности S выбрана верхняя сторона и сама поверхность S задана явно уравнением z = f(x, y), где функция f(x, y) и ее частные производные f’_x и f’_y непрерывны в замкнутой ограниченной области s_ху, являющейся проекцией поверхности S на плоскость Oxy, то направляющие косинусы нормали рассчитываются по формулам аналитической геометрии в пространстве и векторной алгебры:

Если поверхность S задана в неявном виде уравнением F(x, y, z) = 0, то направляющие косинусы нормали к этой поверхности определяются по формулам:

где и выбор знака перед радикалом согласовывается со стороной поверхности.

Вычисление ПИВР

Вычисление поверхностных интегралов второго рода сводится к вычислению двойных интегралов.

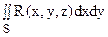
по верхней стороне двусторонней S области, считая, что R(x, y, z)– непрерывная функция на поверхности S. Будем считать, что поверхность S описывается уравнением
z = f(x, y), где f(x, y) – непрерывная функция в замкнутой ограниченной области s_xy, являющейся проекцией поверхности S на плоскость Оху. Тогда интеграл (7) вычисляется по формуле:

Таким образом, для вычисления поверхностного интеграла второго рода по верхней стороне поверхности S следует: используя уравнение поверхности S, заменить у подынтегральной функции переменную z функцией f(x, y) и вычислить полученный двойной интеграл по области s_ху – проекции поверхности S на плоскость Оху.

Интегрирование по нижней стороне поверхности S сводится к интегрированию по верхней стороне после перемены знака перед двойным интегралом в правой части равенства (8).

Аналогично, если функция P(x, y, z) непрерывна на двусторонней поверхности S, заданной уравнением x = j(y, z), где j(y, z) – непрерывная функция в замкнутой ограниченной области r = s_yz, являющейся проекцией поверхности S на плоскость Oyz, то вычисление поверхностного интеграла 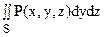по стороне поверхности S, направленной в сторону роста переменной х, сводится к вычислению двойного интеграла по формуле

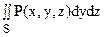Наконец, если функция Q(x, y, z) непрерывна на двусторонней поверхности S, заданной уравнением y = y(x, z), где y(x, z) – непрерывная функция в замкнутой ограниченной области w = s_xz, являющейся проекцией поверхности S на плоскость Oxz, то вычисление поверхностного интеграла по стороне поверхности S, направленной в сторону роста переменной у, сводится к вычислению двойного интеграла в соответствии с формулой:

Пример 4.

Вычислить интеграл по верхней стороне части плоскости
x + 2z = 2, лежащей в первом октанте и отсекаемой плоскостью у = 4.

В соответствии с определением поверхностного интеграла общего вида (*) можем написать:

Разрешив относительно х уравнение плоскости ABCD, в соответствии с формулой (9) имеем для первого интеграла:

где в правой части стоит двойной интеграл по прямоугольнику ОВСЕ, в который проектируется на плоскость Oyz прямоугольник ABCD. Используя правило вычисления двойных интегралов в декартовых координатах, получим:

Так как прямоугольник АВСD является цилиндрической поверхностью с образующими, параллельными оси Oy, то, в согласии со свойством 5 поверхностных интегралов, будем иметь:

Для вычисления третьего интеграла в правой части (11) разрешим уравнение плоскости ABCD относительно z: z = 1 – x/2 и воспользуемся формулой (8):

Вычисляя последний интеграл по прямоугольнику AOED, получим:

Используя результаты вычисления интегралов, входящих в (11), и складывая их, получим окончательно:

Пример 5.

Вычислить , где S – часть поверхности x-y+z=1, образованная ее пересечением с координатными плоскостями. Выбор нормали к поверхности S указан на рис. 4.

Будем вычислять каждый из слагаемых интегралов отдельно. В первом из них надо выразить z через х и у из уравнения плоскости z = 1-x + y, причем перед интегралом по s_xy (т.е. по треугольнику АОВ) надо взять знак плюс, т.к. выбранная нормаль с осью Oz образует острый угол g (cosg > 0):

Аналогично,

Здесь при вычислении I₂ была использована формула (4), причем знак минус взят потому, что выбранная нормаль n образует с осью Oy тупой угол b
(cosb < 0). При вычислении I₃ учитывалась формула (4) и то, что cosa > 0.

Таким образом,

Date: 2016-07-22; view: 1207; Нарушение авторских прав