Приложения криволинейных интегралов.

1. Площадь области D, ограниченной замкнутым контуром L, находится по формуле:

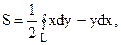
где направление обхода контура L выбрано так, что область D остается все время слева от пути интегрирования.

2. Пусть L есть плоская кривая с линейной плотностью массы m(x, y),
тогда

а) масса m кривой L вычисляется по формуле

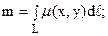
б) координаты центра тяжести кривой L вычисляются по формулам:

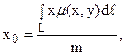
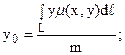
в) моменты инерции I_x, I_y и I₀ соответственно относительно осей Ox, Oy и начала координат равны:

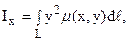
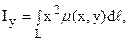
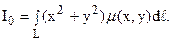(27)

3. Пусть 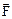= P(x, y, z) 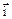+Q(x, y, z) 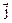+ R(x, y, z) 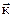есть переменная сила, совершающая работу W вдоль пути L, и функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на кривой L.

Тогда

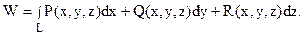
Пример 19.

Найти массу тонкого стержня, имеющего форму линии x² + y² = 1, y > 0, если его линейная плотность в точке M(x, y) равна m(x, y) = 1 + (1/2)y.

В данном случае линия L есть верхняя половина единичной окружности, которую легко задать параметрически: x = cost, y = sint, 0 < t < p. Поэтому, воспользовавшись формулой (25), получим:

Ответ: m = p + 1.

Пример 20.

Вычислить момент инерции пружины, состоящей из n витков, относительно ее оси (предполагается, что пружина изготовлена из однородного материала).

где m(x, y) – линейная плотность пружины.

Ответ:

Пример 21.

Найти работу силы при перемещении точки ее приложения от А(1;1;1) до В(2;3;4) по прямой.

Как известно, работа силы (силового поля) может быть вычислена как интеграл второго рода. Формула (28) для пространственного случая:

Воспользовавшись известными параметрическими уравнениями прямой, запишем уравнения линии, по которой перемещается точка приложения силы:

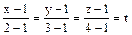Þx = 1 + t, y = 1 + 2t, z = 1 + 3t, 0 < t < 1.

В силу условия, t_нач = 0, t_кон = 1. Тогда

Пример 22.

Вычислить площадь фигуры, ограниченной астроидой x = acos³t,
y = asin³t, 0 < t < 2p (рис. 14).

Из формулы Грина вытекает, что (см. (20,24))

(*)

где K_D – граница области D, проходимая так, чтобы область оставалась слева.

Воспользовавшись этой формулой, получим:

Пример 23.

Вычислить площадь области, ограниченной эллипсом x = acost, y = bsint.

Из формулы (24) следует, что

Пример 24.

Найти массу четверти эллипса x = cost, z = 2sint, расположенной в первом квадранте плоскости xOz, если линейная плотность массы m = z.

Из формулы (25) следует, что

Из уравнения кривой L находим:

Очевидно, что параметр t меняется от 0 до p/2.

Тогда

Положив cost = u, получим:

Пример 25.

Найти координаты центра тяжести однородной дуги циклоиды
x = a(t-sint), y = a(1-cost), если (0 < t < 2p).

В силу симметрии кривой относительно прямой x = ap получаем х₀ = p. Найдем теперь m, а затем y₀. Из уравнения циклоиды находим, что и тогда

Пример 26.

Найти моменты инерции относительно координатных осей и начала координат четверти однородной окружности y = 2cost, z = 2sint, лежащей в первом квадранте плоскости yOz.

В силу одинакового расположения кривой по отношению к координатным осям I_y = I_z. По формулам (27) получаем:

Пример 27.

Вычислить работу силы при перемещении точки массы m из точки О(0;0) в точку А(1;1) по прямой z = y, лежащей в плоскости yOz.

Из формулы (28) следует, что

Так как мы интегрируем по прямой z = y и при перемещении из точки О в точку А y меняется от 0 до 1, получаем:

Date: 2016-07-22; view: 3268; Нарушение авторских прав