Поверхностные интегралы второго рода (по координатам) – ПИВР.

Вначале уточним понятие стороны поверхности. С этой целью рассмотрим гладкую поверхность S, на которой зафиксируем произвольную точку М, проведем через нее нормаль к поверхности S, и выберем на этой нормали одно определенное направление. Проведем на поверхности S произвольный замкнутый контур L, проходящий через точку М и не пересекающий границы поверхности S.

Начнем теперь перемещать точку М по выбранному контуру, приписывая каждому из положений нормали то, в которое непрерывно переходит выбранное вначале направление. При возвращении точки М в исходное положение может случиться одно из двух: либо направление нормали совпадает с исходным, либо же – противоположно ему.

Если на гладкой поверхности S существует хотя бы одна точка и хотя бы один замкнутый, не пересекающий границы поверхности контур L, при обходе по которому направление нормали изменится на противоположное, то поверхность S называется односторонней.

Если для любой точки М поверхности S и любого замкнутого, не пересекающего границы поверхности S контура L, окажется, что после его обхода направление нормали не изменится, то поверхность S называется двусторонней (рис. 2).

Совокупность точек двусторонней поверхности вместе с направлениями нормали, непрерывно переходящими друг в друга, называется стороной поверхности.

Для двусторонней поверхности выбор направления нормали в одной ее точке определяет направление нормалей во всех точках поверхности.

Примерами двусторонних поверхностей могут служить любая плоскость, сфера, эллипсоид, параболоид, любая поверхность, задаваемая уравнением
z = f(x, y), где f(x, y), f’_x(x, y), f’_y(x, y) – непрерывные функции в некоторой области плоскости Оху и т.д.

Примером односторонней поверхности может служить лист Мебиуса. В дальнейшем мы будем рассматривать только двусторонние поверхности.

Пусть S – незамкнутая гладкая двусторонняя поверхность, ограниченная контуром L, не имеющим точек самопересечения. Выберем определенную сторону этой поверхности. Будем называть положительным направлением обхода контура L такое, при движении по которому наблюдатель, находящийся на выбранной стороне поверхности, видит саму поверхность S слева от себя. Направление обхода, обратное положительному, называется отрицательным. Легко видеть, что выбор положительного направления обхода контура L поверхности S однозначно определяет ее сторону, и наоборот.

Перейдем теперь к определению поверхностного интеграла второго рода. Пусть в пространстве Oxyz имеется двусторонняя поверхность S, заданная (для определенности) уравнением вида z = f(x, y). Выберем определенную сторону поверхности. Пусть также в точках поверхности задана функция F(x, y, z). Проделаем 5 операций:

1. Разобъем поверхность S на n частей (частичных поверхностей) не имеющих общих внутренних точек, а диаметры этих частей обозначим через l₁, l₂,…, l_n, причем наибольший из диаметров обозначим через l и назовем его рангом дробления. Обозначим через DS_k^(xy) (k = 1, 2, …, n) площадь проекции k-той частичной поверхности на плоскость Оху, взятую со знаком плюс, если нормаль к ней в выбранную сторону поверхности образует с осью Oz острый угол, и со знаком минус, если нормаль в выбранную сторону поверхности образует с осью Oz тупой угол.

2. В каждой частичной поверхности выберем произвольно по точке
(х_к; у_к; z_к) и вычислим в них значения функции F(x, y, z), т.е. найдем числа
F(x_k, y_k, z_k).

3. Вычислим произведения F(х_k, у_k, z_k)D

4. Составим сумму и назовем её интегральной суммой для функции F(x, у, z) по переменным х и у по выбранной стороне поверхности S, отвечающей произведенному дроблению на части DS_k и выбору точек (х_k; у_k; z_k).

5. Измельчая дробление, ищем предел

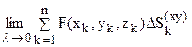
Если существует конечный предел (5), не зависящий ни от способа дробления области S на части, ни от выбора точек (x_k; у_k; z_k), то этот предел называют поверхностным интегралом второго рода (ПИВР) по выбранной стороне поверхности S от функции F(х, у, z) по переменным х и у и обозначают символом

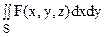(6)

(Здесь dxdy напоминает о площади проекции элемента поверхности S на координатную плоскость Оху). Легко видеть, что в символе (6) нет указания на то, какая сторона поверхности имеется в виду, поэтому это указание дается в тексте постановки конкретной задачи специально.

Если элементы разбиений поверхности S проектировать не на плоскость Оху, а на плоскость Оyz или Оxz, то аналогичным образом можно определить поверхностные интегралы второго рода по выбранной стороне поверхности S соответственно по переменным у и z или х и z, приняв по определению:

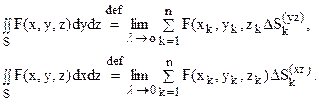
Перечислим простейшие свойства поверхностного интеграла второго рода.

1. При перемене стороны поверхности поверхностный интеграл второго рода изменяет знак.

2. Постоянный множитель в подынтегральной функции можно выносить за знак поверхностного интеграла:

3. Поверхностный интеграл второго рода от суммы функций равен сумме интегралов от этих функций:

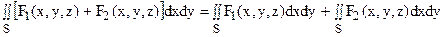
4. Если поверхность S разбита на части, то поверхностный интеграл по всей поверхности S равен сумме интегралов по ее частям, так, если S=S₁+S₂,то:

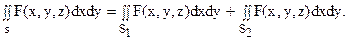
5. Если S- цилиндрическая поверхность с образующими, параллельными оси OZ, то (так как поверхность проектируется на ХОУ в линию, а площадь линии равна нулю).

В приложениях часто встречается ситуация (см. КИВР), когда в точках поверхности S определены три функции Р(х, у, z), Q(x, y, z) и R(x, y, z) и рассматривается поверхностный интеграл второго рода «общего вида» по выбранной стороне поверхности S, обозначаемый символом:

и определяемый равенством:

(*)

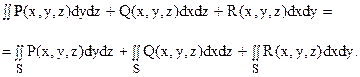Date: 2016-07-22; view: 531; Нарушение авторских прав