Условия независимости криволинейных интегралов от формы пути интегрирования ( условия НПИ).

где А и В – произвольные точки из области s, а АВ – произвольная кусочно-гладкая кривая, целиком лежащая в области s. Может случиться, что интеграл (21) зависит лишь от координат точек А(x₀; y₀) и B(x₁; y₁), а от формы кривой АВ, целиком лежащей в s, не зависит.

В этом случае его называют криволинейным интегралом, не зависящим от пути интегрирования (точнее, от формы этого пути) в области s и обозначают символом

или .

Возникает вопрос: какие условия должны быть выполнены, чтобы интеграл (21) не зависел от пути интегрирования в области s?

Оказывается, что если функции P(x, y) и Q(x, y) определены и непрерывны вместе со своими частными производными ¶Q/¶x и ¶P/¶y в односвязной и открытой области s, то следующие 4 утверждения равносильны:

1. Криволинейный интеграл 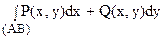зависит лишь от точек А и В, а от кривой АВ, целиком лежащей в области s, не зависит.

2. Для любого замкнутого контура L, целиком лежащего в области s,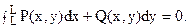

3. Всюду в области s выполняется тождество .

4. Выражение P(x, y)dx + Q(x, y)dy является полным дифференциалом некоторой функции u(x, y) в области s.

Если условия 1-4 выполняются, то криволинейный интеграл второго рода удобно вычислять по формуле:

Эта формула получается, если за путь интегрирования взять ломаную АСВ, звенья которой параллельны осям координат (см. рис. 8). Формулу (21А) запоминать не надо: понимая ее суть, нужно в каждой конкретной задаче двигаться от начальной точки А к конечной точке В вдоль отрезков, параллельных осям координат.

Аналогичные утверждения имеют место и для интеграла

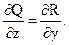
Функцию u = u(x, y) (см. п.4) часто называют потенциальной (первообразной) функцией для дифференциального выражения Pdx+ Qdy. Она может быть найдена по формуле (см. 21А):

где (x₀; y₀) – любая фиксированная точка области s; (x; y) – переменная текущая точка; С – произвольная постоянная.

Из формулы (22) следует, что криволинейный интеграл равен разности значений потенциальной функции в конечной и начальной точках пути интегрирования, т.е.

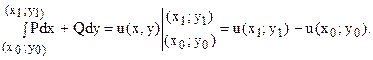
Пример 13.

Вычислить интеграл , где АВ – верхняя половина окружности
x² + y² = 4, пробегаемая от точки А (-2;0) до точки В (2;0) (рис. 9).

Заметим вначале, что функции P(x,y) = x² и Q(x, y) = y² непрерывны и дифференцируемы на плоскости Oxy, а затем вычислим производные ¶Q/¶x и ¶P/¶y. Получим:

Следовательно, искомый интеграл не зависит от пути интегрирования. Заменим дугу АВ отрезком АВ оси Ox. В этом случае y = 0, dy = 0 и, следовательно,

Пример 14.

Вычислить интеграл от А(1;1) до В(0;0) по линии L:

Попытка вычисления данного интеграла вдоль линии со столь сложным уравнением любым из рассмотренных выше способов приведет к немалым, а главное, неоправданным, трудностям.

В некоторых достаточно часто встречающихся в приложениях случаях криволинейный интеграл второго рода может быть вычислен по формуле, являющейся обобщением формулы Ньютона-Лейбница.

Если Pdx + Qdy является полным дифференциалом некоторой функции H = H(x,y), т.е. dH = Pdx + Qdy,

В нашем случае поэтому по формуле (23)

Пример 15.

Вычислить интеграл , где 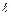– верхняя половина окружности x² + z² = 4, пробегаемая по ходу часовой стрелки и лежащая в плоскости xOz.

В данном случае P = x², Q = z², и так как 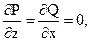то результат интегрирования не зависит от пути.

Интегрирование по верхней половине окружности заменим интегрированием по отрезку оси Ox, соединяющему точки пересечения окружности
А (-2;0) и В (2;0) с осью Ох. На этом отрезке z = 0 и dz = 0, а х меняется от –2 до 2. Следовательно,

Пример 16.

Вычислить интеграл , где 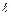– окружность (x-1)² + (y-1)² = 1, пробегаемая против хода часовой стрелки.

Контур 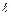замкнутый:

, ,

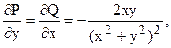
поэтому по формуле Грина данный интеграл равен нулю.

Пример 17.

Показать, что есть полный дифференциал некоторой функции и восстановить эту функцию.

P’_y = -(x + y)^-2, Q’_x = -(x + y)^-2, т.е. условие 3 выполнено.

В то же время P, Q, P’_y и Q’_х – элементарные функции и потому непрерывны всюду, где определены, т.е. вне прямой y = -x. Поэтому является полным дифференциалом в любой односвязной области D, не пересекающейся с прямой
y = -x. Возьмем, например, в качестве области D верхнюю полуплоскость, ограниченную
y = -x, и восстановим функцию, дифференциалом которой является заданное выражение. Для этого фиксируем в Dкакую-нибудь точку, например, А(1;1). Тогда в произвольной точке В(X;Y) значение искомой функции Н может быть вычислено с помощью криволинейного интеграла по формуле (19):

Так как данный интеграл не зависит от пути интегрирования в силу условия Q’_x = P’_y, он может быть вычислен, например, по линии, состоящей из отрезков, параллельных осям координат:

Учитывая, что на АС y = const = 1,а х меняется от1 до Х, имеем:

На СВ x = X = const, а y меняется от1 до Y, поэтому имеем:

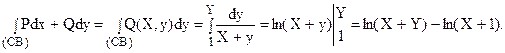
Таким образом,

H(X, Y) = H(B) = H(A) + ln(X+1) – ln2 + ln(X+Y) – ln(X+1) = H(A) – ln2 + ln(X+Y).

Или, в привычных обозначениях:

H(x, y) = ln(x+y) + C, где C = H(A) – ln2.

Константа С может быть произвольной, так как функции, отличающиеся на постоянную, имеют равные дифференциалы.

Ответ: H(x, y) = ln(x+y) + C.

Пример 18.

(проверить НПИ).

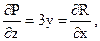
Date: 2016-07-22; view: 614; Нарушение авторских прав