Поверхностные интегралы первого рода (по площади поверхности).

Поверхностные интегралы первого рода (ПИПР) представляют собой одно из возможных обобщений двойных интегралов.

Пусть в пространстве Oxyz задана гладкая поверхность S, в точках которой определена произвольная функция F(x, y, z). (Поверхность называется гладкой, если в каждой точке существует касательная плоскость, непрерывно изменяющаяся вдоль поверхности). Проделаем 5 операций.

1. Разобьем поверхность S на n частей, не имеющих общих внутренних точек. Обозначим площади и диаметры этих частей соответственно через Ds₁, Ds₂,…, Ds_n и l₁, l₂,…, l_n. Наибольший из диаметров обозначим через l и назовем рангом дробления.

2. В каждой частичной области выберем произвольным образом по точке (x_k; y_k; z_k) и вычислим в них значения функции F(x, y, z), т.е. найдем числа F(x_k, y_k, z_k).

3. Вычислим произведения F(x_k, y_k, z_k) Ds_k (k = 1, 2, …, n).

4. Найдем сумму которую называют интегральной суммой для функции F(x, y, z) по поверхности S, отвечающей произведенному дроблению на части и выбору точек (x_k; y_k; z_k).

5. Измельчая дробление, ищем предел

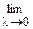
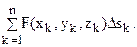
При этом функцию F(x, y, z) называют подынтегральной функцией, a S – поверхностью интегрирования, ds – элементом площади поверхности S.

Таким образом, по определению

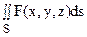
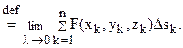
Простейшие свойства поверхностного интеграла первого рода:

1. Если F(x, y, z) = 1 в любой точке поверхности S, то 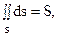где S – площадь поверхности интегрирования.

2. Постоянный множитель К подынтегральной функции можно выносить за знак поверхностного интеграла:

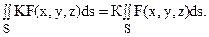
3. Поверхностный интеграл первого рода от суммы двух функций равен сумме интегралов от этих функций:

4. Если поверхность S разбита на две части S₁ и S₂, то поверхностный интеграл по всей поверхности равен сумме интегралов по ее частям:

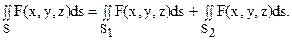
5. Если в точке А поверхности S функции F₁(x, y, z) и F₂(x, y, z) удовлетворяют неравенству F₁(x, y, z) < F₂(x, y, z), то

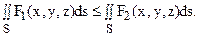
6. Имеет место неравенство:

7. (Теорема о среднем). Если функция F(x, y, z) непрерывна на поверхности S, то на этой поверхности найдется хотя бы одна такая точка , что будет иметь место равенство: где S – площадь поверхности S.

Если на поверхности S распределена с плотностью m(x, y, z) некоторая масса m, то 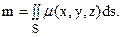Координаты центра масс, статические моменты и моменты инерции материальной поверхности вычисляются по формулам, аналогичным формулам, приведенным в разделе «Двойные интегралы», т.к. (мы это ниже увидим), вычисление поверхностных интегралов первого рода сводится к вычислению двойных интегралов.

Обозначим через s_xy проекцию поверхности S на плоскость Oxy. Рассмотрим случай, когда s_xy – замкнутая ограниченная область, а поверхность S такова, что она может быть задана уравнением z = f(x, y), где функция f(x,y) вместе с частными производными f’_x и f’_y непрерывна в s_xy. Тогда формула для вычисления поверхностного интеграла первого рода для случая, когда функция F(x, y, z) непрерывна на поверхности S, имеет вид:

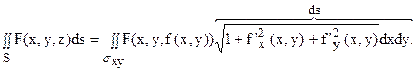
Таким образом, для вычисления поверхностного интеграла первого рода по поверхности S следует: используя уравнение z = f(x, y) поверхности S, заменить у подынтегральной функции переменную z функцией f(x, y), а элемент площади ds – произведением 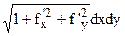и вычислить полученный двойной интеграл по области s_xy – проекции поверхности S на плоскость Oxy.

Естественно, что имеют место еще две формулы, соответствующие проектированию поверхности S на плоскости Oyz и Oxz.

Если различные участки поверхности S заданы различными уравнениями, то нужно разбить поверхность S на соответствующие части и весь интеграл вычислять как сумму интегралов, взятых по этим частям.

Пример 1.

Вычислить , где S – часть плоскости x + y + z – 1 = 0, лежащая в первом октанте.

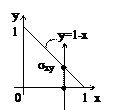
Поверхность S проектируется на плоскость Oxy в область s_xy, представляющую собой треугольник (рис. 1).

Разрешив уравнение данной плоскости относительно z, получим:

z = 1-x-y.

Таким образом, в нашем случае f(x, y) = 1-x-y и, следовательно, f’_x(x, y) = -1, f’_y(x, y) = = -1.

Непосредственно видно, что все они непрерывны в s_xy и, значит, в соответствии с формулой (4) можем написать:

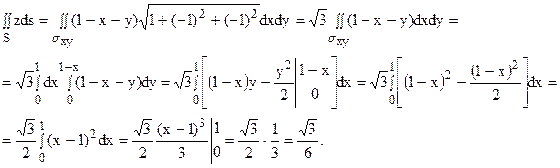
Пример 2.

Вычислить где s – часть плоскости x + y + z = 1, заключенная в первом октанте (см. рис. 1).

Запишем уравнение данной плоскости в виде z = 1-x-y. Так как
¶z/¶x = -1, ¶z/¶y = -1, то по формуле (4)

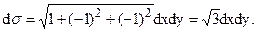
Проекцией s на плоскость xOy является треугольник D, ограниченный прямыми x+y=1, x = 0, y = 0. В этом треугольнике х меняется от 0 до 1, а при каждом фиксированном х ордината меняется от y = 0 до y = 1-x. Поэтому по формуле (4) имеем:

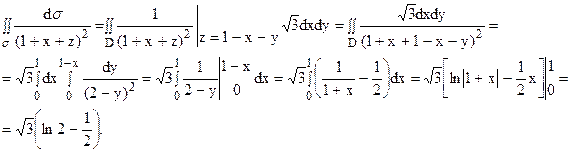
Пример 3.

Вычислить координаты центра тяжести С однородной полусферы радиуса R.

Выберем систему координат так, чтобы полусфера стояла на плоскости xOy, а начало координат находилось в ее центре. Тогда уравнение полусферы будет иметь вид
x² + y² + z² = R² (z > 0). Так как поверхность однородная (постоянная плотность массы), то из соображений симметрии ее центр тяжести должен находиться на оси Oz, т.е. x_C = 0,
y_C = 0. Формула для вычисления z_C однородной поверхности s имеет вид:

В данном случае поверхность s задана уравнением x² + y² + z² = R² (z > 0), откуда 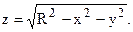Вычисляя по формуле (4) элемент поверхности сферы, получим (проверьте!)

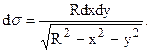
Данная полусфера проектируется в круг D радиуса R с центром в начале координат, поэтому

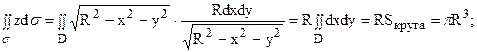
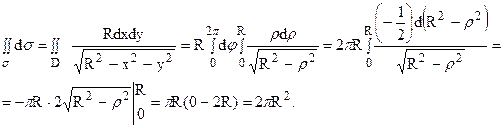
Для вычисления второго интеграла были применены полярные координаты на плоскости xOy.

Таким образом, окончательно для координаты z_C получаем:

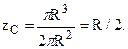
Date: 2016-07-22; view: 1211; Нарушение авторских прав