
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи для самостоятельного решения.
|
|
В задачах 1  5 восстановить область интегрирования и изменить порядок интегрирования; сделать чертеж.
5 восстановить область интегрирования и изменить порядок интегрирования; сделать чертеж.
1.  2.
2. 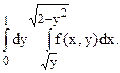
3.  4.
4. 
5. 
В задачах 6  10 перейти от двойного интеграла к повторному двумя способами и сделать чертеж области интегрирования D.
10 перейти от двойного интеграла к повторному двумя способами и сделать чертеж области интегрирования D.
6. D: x ³ y2-1; x2+y2 £ 1. 7. D: y £ -x+2; y ³ x -2; 0 £ x £ 1
8. D: y £ x2+1; y ³ 0; -1 £ x £ 1. 9. D: y ³ x; y ³ -x; y £ -x2+2.
10. D: y £ x; x2+y2 £ 2x; y ³ 0.
11. Найти абсциссу хс центра масс однородной пластины, ограниченной линиями х2+у2=2у, х2+у2=4, у=0 (х ³ 0).
12. Найти площадь области, заданной неравенствами: х2+у2 ³ 2; х2+у2 £ 2у.
13. Найти площадь части поверхности конуса z2=3х2+3y2, содержащейся между цилиндром х2+у2=4 и плоскостью у=1 (у ³ 1, z ³ 0).
14. Найти момент инерции относительно оси Оу пластины, заданной неравенствами х2+у2£2х, х ³ 1, у ³ 0, если ее плотность 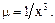
15. Найти массу пластины, ограниченной линиями: х2+у2=1, х+у=1 (х ³ 0), если ее плотность 
16. С помощью двойного интеграла найти объем тела, ограниченного цилиндром z=у2+2 и плоскостями у=0, z=0, у-х=1, у+х=1.
17. Найти площадь поверхности части цилиндра  лежащую между плоскостями z=2, у=х, у=2х (х³0).
лежащую между плоскостями z=2, у=х, у=2х (х³0).
18. Найти момент инерции относительно оси Ох однородной пластины (плотность  =1), ограниченной линиями у=ех, х=0, х=1, у=0.
=1), ограниченной линиями у=ех, х=0, х=1, у=0.
19. С помощью двойного интеграла найти объем тела, ограниченного поверхностями у=х2, z=х2+у2, у=1, z=0.
20. Найти массу пластины, ограниченной линиями у=–х2+1, у=х+1, у=3х-3, если ее плотность 
21. Найти массу тела, ограниченного поверхностями z=8-х2-у2, х+у=2, х=0, у=1, z=0 и имеющего плотность 
22. Найти массу тела, ограниченного поверхностями (z-4)2=x2+y2, y=1-x2, y=0, z=0 и имеющего плотность 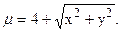
23. Найти массу тела, ограниченного поверхностями  х+у+z=2, у=0, z=0 и имеющего плотность
х+у+z=2, у=0, z=0 и имеющего плотность  =2.
=2.
24. Найти массу тела, ограниченного поверхностями  z=4-х2, z=0, у=1 и имеющего плотность
z=4-х2, z=0, у=1 и имеющего плотность 
25. Найти массу тела, ограниченного поверхностями х+у+z=4, х+у-z=4, х=0, у=0 и имеющего плотность m=5+z.
26. Найти массу тела, ограниченного поверхностями z=1-x2, х2+у2=2у, х=0, z=0 (х ³ 0) и имеющего плотность 
27. Найти массу тела, ограниченного поверхностями х2+у2=(z-2)2, z=0, х=1 и имеющего плотность 
28. Найти массу тела, ограниченного поверхностями х2+у2=2х, х2+у2+z2=4
(х ³ 0) и имеющего плотность  =1.
=1.
29. Найти массу тела, ограниченного поверхностями z= х2+у2-1, х+у=2, х=0, у=0, z=0 и имеющего плотность, заданную выражением 
30. Найти массу тела, ограниченного поверхностями х2+у2-z2=–1, х2+у2=1, у=х, у=–х, х=2 и имеющего плотность 
В задачах 31  35 изменить порядок интегрирования в повторном интеграле и изобразить область интегрирования графически.
35 изменить порядок интегрирования в повторном интеграле и изобразить область интегрирования графически.
31.  32.
32. 
33. 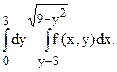 34.
34. 
35. 
В задачах 36  40 расставить двумя способами пределы интегрирования в повторном интеграле по заданной области D. Сделать чертеж.
40 расставить двумя способами пределы интегрирования в повторном интеграле по заданной области D. Сделать чертеж.
36. D: y ³ x; 2x+y ³ 0; y £ 2. 37. х2+у2 £ 25; 0 £ x £ 3.
38. D: x+y ³ 0; х2+у2 £ 4; x ³ 0. 39. D: x ³ y2; x+2y³0; x £ 4.
40. D: y £ x+1; x £ 1-y2.
В задачах 41  45 с помощью двойного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
45 с помощью двойного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
41. х=0, у=0, z=0, х=3, у=3, z=х2+у2.
42. х=0, z=0, z=4-х2-у2.
43. х=0, z=0, 4х+3у=12, 
44. х=0, z=0, 2х+у=4, z=4-х2.
45. х=0, у=0, z=0; х=4, у=4, х+у+z=8.
46. Найти площадь части поверхности х2+у2+z2=25, вырезанной поверхностями х2+у2=16 и у=0 (у ³ 0). При вычислении двойного интеграла перейти к полярным координатам.
47. Найти площадь части поверхности 8z=х2+у2, вырезанной поверхностями х2+у2=9, у=0, у=х (х ³ 0, у ³ 0).
48. Найти площадь части поверхности z2= х2+у2, вырезанной поверхностями z=1, z =4.
49. Найти площадь части поверхности 8z=9- х2-y2, расположенной в первом октанте
(х ³ 0, у ³ 0, z ³ 0). При вычислении двойного интеграла перейти к полярным координатам.
50. Найти площадь части поверхности х2+у2+z2=169, вырезанной поверхностями z=5 и z=12.
В задачах 51  60 найти массу тела, имеющего плотность
60 найти массу тела, имеющего плотность  и ограниченного указанными поверхностями. Сделать чертеж.
и ограниченного указанными поверхностями. Сделать чертеж.
51. x=0, y=0, z=0, x+y+z=3;  =y.
=y.
52. x=0, y=0, z=0, x+y+z=6;  =z.
=z.
53. z=9-x2-y2, x=0, z=0(x³0);  =x (перейти к цилиндрическим координатам).
=x (перейти к цилиндрическим координатам).
54. z=x2+y2, z=4;  =z.
=z.
55. z=5-x2-y2, z=1;  =x2+y2 (перейти к цилиндрическим координатам).
=x2+y2 (перейти к цилиндрическим координатам).
56. x2+y2+z2=25, x=0, y=0, z=3;  =z (z³3);
=z (z³3);
перейти к цилиндрическим координатам.
57. z2=x2+y2, x=0, y=0, z=2 (x³0, y³0);  =xy;
=xy;
перейти к цилиндрическим координатам.
58. x2+y2+z2=4, x2+y2=4, z=2 (z³0);  =z;
=z;
перейти к цилиндрическим координатам.
59. x2+y2+z2=9, x2+y2+z2=1;  ;
;
перейти к сферическим координатам.
60. x2+y2+z2=4, z2=x2+y2, 
 ;
;
перейти к сферическим координатам.
В задачах 61  65 изменить порядок интегрирования в повторном интеграле; сделать чертеж области интегрирования.
65 изменить порядок интегрирования в повторном интеграле; сделать чертеж области интегрирования.
61. 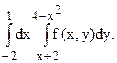 62.
62. 
63.  64.
64. 
65. 
В задачах 66  70 перейти от двойного интеграла
70 перейти от двойного интеграла 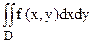 к повторному двумя способами; сделать чертеж области интегрирования D, заданной системой неравенств.
к повторному двумя способами; сделать чертеж области интегрирования D, заданной системой неравенств.
66.  67.
67. 
68.  69.
69. 
70. 
71. Найти площадь части поверхности  вырезанной поверхностями х=2, у=х, у=2х.
вырезанной поверхностями х=2, у=х, у=2х.
72. Найти площадь части поверхности у+z=9, вырезанной поверхностями у=х2и z=0 при z³0.
73. Найти площадь части поверхности  вырезанной поверхностями х2+у2=3 и х=0 при х³0.
вырезанной поверхностями х2+у2=3 и х=0 при х³0.
74. Найти площадь части сферы  вырезанной поверхностями у=0,
вырезанной поверхностями у=0,  z=0 и расположенной в первом октанте.
z=0 и расположенной в первом октанте.
75. Найти площадь части поверхности  заключенной между плоскостями z=1, z=3, у=0 при у³0.
заключенной между плоскостями z=1, z=3, у=0 при у³0.
В задачах 76  80 необходимо найти объем тела, ограниченного заданными поверхностями:
80 необходимо найти объем тела, ограниченного заданными поверхностями:
76. 
77. 
78. 
79. 
80. 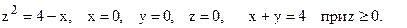
В задачах 81  83 вычислить двойной интеграл по области
83 вычислить двойной интеграл по области  ; сделать чертеж области
; сделать чертеж области  .
.
81. 
82. 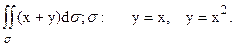

83. 
84. Перейти от двойного интеграла  к повторному, взяв за переменную интегрирования во внутреннем интеграле переменную х, если
к повторному, взяв за переменную интегрирования во внутреннем интеграле переменную х, если
D: х3 £ у £ 1, х+у ³ –2. Сделать чертеж области 
85. Условия задачи 84, но внутреннее интегрирование произвести по переменной у.
86. Изменить порядок интегрирования в повторном интеграле  . Сделать чертеж области интегрирования.
. Сделать чертеж области интегрирования.
87. Вычислить  D: у=х2, у=2-х; сделать чертеж области интегрирования
D: у=х2, у=2-х; сделать чертеж области интегрирования 
88. Найти площадь области D, заданной системой неравенств: 
Расставить двумя способами пределы интегрирования, если область интегрирования в задачах 89,90 задана системой неравенств; сделать чертеж.
89. 
90. 
В задачах 91  100 вычислить двойной интеграл по области D, заданной системой неравенств.
100 вычислить двойной интеграл по области D, заданной системой неравенств.
91. 
92. 
93. 
94. 
95. 
96. 
97. 
98. 
99. 
100. 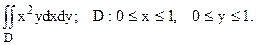
В задачах 101  111 расставить двумя способами пределы интегрирования в двукратном интеграле при заданной области интегрирования D; сделать чертеж области D.
111 расставить двумя способами пределы интегрирования в двукратном интеграле при заданной области интегрирования D; сделать чертеж области D.
101. D: x=3; x=5; 3x-2y+4=0; 3x-2y+1=0.
102. D: x=0; y=0; x+y=2.
103. D: x2+y2£1; x³0; y³0.
104. D: x+y£1; x-y£1; x³0.
105. D: y³x2; y£4-x2.
106. D: 9x2+4y2£36.
107. D: (x-2)2+(y-3)2£4.
108. D: y=x2; y= 
109. D: y=x; y=2x; x+y=6.
110. D: y=x; y=x+3; y=–2x+1; y=–2x+5.
111. D: y2-x2=1; x2+y2=9.
В задачах 112  124 изменить порядок интегрирования в повторном интеграле; построить область интегрирования.
124 изменить порядок интегрирования в повторном интеграле; построить область интегрирования.
112. 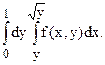 113.
113. 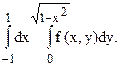
114.  115.
115. 
116. 
 117.
117. 
118. 
119. 
120. 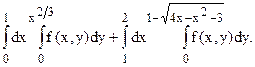
121. 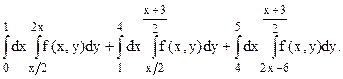
122. 
123. 
124. 
В задачах 125  130 вычислить двойной интеграл; сделать чертеж области интегрирования D.
130 вычислить двойной интеграл; сделать чертеж области интегрирования D.
125. 
126. 
127. 
128. 
129. 
130. 

В задачах 131  140 вычислить площадь области интегрирования D в двойном интеграле; область D задана уравнениями ограничивающих ее линий в плоскости хОу; построить область графически.
140 вычислить площадь области интегрирования D в двойном интеграле; область D задана уравнениями ограничивающих ее линий в плоскости хОу; построить область графически.
131. xy=4; y=x; x=4. 132. y=x2; 4y=x2; y=4.
133. y=x2; 4y=x2; x=±2. 134. y2=4+x; x+3y=0.
135. y=lnx; x-y=1; y=–1. 136. y=sinx; y=cosx; x=0.
137. y=x2; y=x+2. 138. y=4-x2; y=x+2.
139. 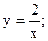
 x=4. 140. x £ y;
x=4. 140. x £ y; 
В задачах 141  147 вычислить двумя способами двойной интеграл по заданной области интегрирования D; построить D.
147 вычислить двумя способами двойной интеграл по заданной области интегрирования D; построить D.
141. 
142. 
143. 
144. 
145. 
146. 
147. 
В задачах 148  150 изменить порядок интегрирования в повторном интеграле; сделать чертеж области интегрирования.
150 изменить порядок интегрирования в повторном интеграле; сделать чертеж области интегрирования.
148.  149.
149. 
150. 
В задачах 151  160 вычислить площадь области интегрирования D в двойном интеграле; область D задана уравнениями ограничивающих ее линий в плоскости хОу или системой неравенств; сделать чертеж области D.
160 вычислить площадь области интегрирования D в двойном интеграле; область D задана уравнениями ограничивающих ее линий в плоскости хОу или системой неравенств; сделать чертеж области D.
151. x=4y-y2; x+y=6.
152. y=2-x2; y=x.
153. 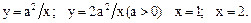
154. 
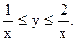
155. 
156. 
157. 
158. 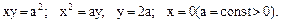
159. 
160. 
161. Привести  к повторному двумя способами, если D: 2y=x, y=2x, x=p; сделать чертеж D.
к повторному двумя способами, если D: 2y=x, y=2x, x=p; сделать чертеж D.
162. Изменить порядок интегрирования в повторном интеграле 
163. Вычислить 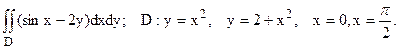
164. Вычислить площадь области 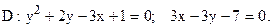
165. Вычислить объем тела, ограниченного поверхностями: z=4-x2, y=0, y=3, z=0.
166. Вычислить массу пластинки D:y=x, y=x+3, x=0, x=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
167. Вычислить статический момент относительно оси Ох пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
168. Вычислить статический момент относительно оси ординат пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
169. Вычислить координаты центра масс пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
170. Найти момент инерции относительно оси абсцисс пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
171. Найти момент инерции относительно оси ординат пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
172. Найти момент инерции относительно начала координат пластины D, ограниченной линиями: у=х, у=х+3, х=0, х=1, если ее плотность  (х,у) равна в каждой точке сумме координат точки.
(х,у) равна в каждой точке сумме координат точки.
В задачах 173  176 перейти от двойного интеграла
176 перейти от двойного интеграла  к повторному для заданной области интегрирования D двумя способами. Сделать чертеж D.
к повторному для заданной области интегрирования D двумя способами. Сделать чертеж D.
173. D: x+y=7; xy=6. 174. D: y=x2; 4-y=x2.
175. D: y2=4-x; y2=x. 176. D:  x=0; x=1; y=1.
x=0; x=1; y=1.
В задачах 177  180 изменить порядок интегрирования в повторном интеграле. Сделать чертеж области D.
180 изменить порядок интегрирования в повторном интеграле. Сделать чертеж области D.
177.  178.
178. 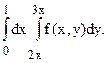
179.  180.
180. 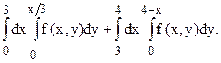
В задачах 181  184 вычислить
184 вычислить  для заданных D и f(x,y). Сделать чертеж области D.
для заданных D и f(x,y). Сделать чертеж области D.
181. 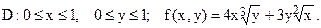
182. 
183. 
184. 
185. Вычислить массу пластины D с вершинами в точках (0;0), ( ;0), (0;1), если плотность
;0), (0;1), если плотность 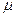 (х,у) равна в каждой точке квадрату расстояния от точки до вершины прямого угла.
(х,у) равна в каждой точке квадрату расстояния от точки до вершины прямого угла.
186. Вычислить статический момент Sх пластины из задачи 185.
187. Вычислить статический момент Sy пластины из задачи 185.
188. Вычислить абсциссу центра масс пластины из задачи 185.
189. Вычислить ординату центра масс пластины из задачи 185.
190. Определить момент инерции Iх фигуры, ограниченной линиями у=2х-х2, у=х2, если плотность в каждой точке численно равна ее ординате.
191. Определить момент инерции Iу пластины из задачи 190.
192. Определить момент инерции I0 пластины из задачи 190. 
193. Вычислить  D: x2+y2=1.
D: x2+y2=1.
194. Вычислить  D: x2+y2=1, x2+y2=4.
D: x2+y2=1, x2+y2=4.
195. Привести  к трехкратному, если V: z=x2+y2, z=2-x2-y2.
к трехкратному, если V: z=x2+y2, z=2-x2-y2.
196. Вычислить 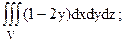 ; V: z=y2, z+2x=6, x=0, z=4.
; V: z=y2, z+2x=6, x=0, z=4.
197. Вычислить объем тела, образованного поверхностями y=2x2, z=0, z=3, 3y+2z=12.
198. Вычислить массу тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2 (x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
199. Вычислить статический момент относительно плоскости хОу тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
200. Вычислить статический момент относительно плоскости хОz тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
201. Вычислить статический момент относительно плоскости уОz тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
202. Вычислить абсциссу центра масс тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
203. Вычислить ординату центра масс тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
204. Вычислить аппликату центра масс тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
205. Найти момент инерции относительно координатной плоскости хОу тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0,
z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
206. Найти момент инерции относительно координатной плоскости хОz тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0,
z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
207. Найти момент инерции относительно координатной плоскости yОz тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
208. Найти момент инерции относительно оси абсцисс тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
209. Найти момент инерции относительно оси ординат тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2 (x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
210. Найти момент инерции относительно оси аппликат тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=0, y=2(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z)=ху2.
(х,у,z)=ху2.
211. Найти момент инерции относительно начала координат тела, ограниченного поверхностями z=2x2, z=3-x2, x=0, y=2, y=0(x ³ 0, y ³ 0, z ³ 0), если в каждой точке тела плотность  (х,у,z) = ху2.
(х,у,z) = ху2.
В задачах 212  215 заданы пространственная область V и функция f(x,y,z) в ней. Начертить область V и вычислить
215 заданы пространственная область V и функция f(x,y,z) в ней. Начертить область V и вычислить 
212. 
213. 
214. 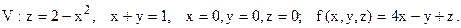
215. 
216. Вычислить объем тела, ограниченного поверхностями 2х+3у=12, 2z=у2, х=0, z=0.
217. Вычислить массу тела, образованного поверхностью х-у+z=1 и координатными плоскостями, если его плотность  (х,у,z) в каждой точке равна абсциссе этой точки.
(х,у,z) в каждой точке равна абсциссе этой точки.
218. Вычислить  где V: x2+y2=1, z=x2+y2, z=0.
где V: x2+y2=1, z=x2+y2, z=0.
219. Вычислить 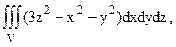 где V: x2+y2+z2=R2.
где V: x2+y2+z2=R2.
220. Вычислить 
221. Построить повторный интеграл для области интегрирования D: y2-x2=1, x=2,x=–2.
В задачах 222  229 вычислить интеграл.
229 вычислить интеграл.
222.  223.
223. 
224.  225.
225. 
226.  227.
227. 
228.  229.
229. 
В задачах 230  237 построить двумя способами в декартовой прямоугольной системе координат двукратный интеграл для заданных областей интегрирования D.
237 построить двумя способами в декартовой прямоугольной системе координат двукратный интеграл для заданных областей интегрирования D.
230. Вершины фигуры D находятся в точках: О(0;0), А(2;0), В(2;1), С(0;1).
231. Вершины фигуры D находятся в точках: О(0;0), А(1;0), В(1;1).
232. Вершины фигуры D находятся в точках: О(0;0), А(2;0), В(1;1), С(0;1).
233. Вершины фигуры D находятся в точках: А(1;2), В(2;4), С(2;7), D (1:5).
234. D – круговой сектор ОАВ с центром в точке О(0;0), у которого концы дуги: А(1;1), В(-1;1).
235. D – параболический сегмент, ограниченный параболой АОВ и отрезком прямой ВА, соединяющей точки В (-1;2) и А (1;2). Точка О (0;0).
236. D – круговое кольцо, ограниченное окружностями радиусов r=1 и R=2 с общим центром О (0;0).
237. D ограничена кривыми у2-х2=1, х2+у2=9 (включает начало координат).
В задачах 238  242 расставить пределы интегрирования в двукратном интеграле двумя способами, если область интегрирования D задана неравенствами.
242 расставить пределы интегрирования в двукратном интеграле двумя способами, если область интегрирования D задана неравенствами.
238. D: x ³ 0, y ³ 0, x+y £ 1.
239. D: y ³ x, x ³ -1, y £ 1.
240. D: x2+y2 £ a2, где а=const > 0.
241. D: x2+y2 £ x.
242. D: y £ x £ y+2a; 0 £ y £ a, где а=const > 0.
В задачах 243  249 изменить порядок интегрирования в двукратном интеграле.
249 изменить порядок интегрирования в двукратном интеграле.
243. 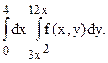 244.
244. 
245.  a>0. 246.
a>0. 246.  a>0
a>0
247.  a>0 248.
a>0 248. 
249. 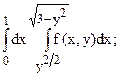
В задачах 250  256 вычислить
256 вычислить  для заданных подинтегральных функций и областей интегрирования.
для заданных подинтегральных функций и областей интегрирования.
250. f(x,y) = x; область D задана вершинами: О (0,0), А (1,1), В (0,1), соединенными отрезками прямых линий.
251. f(x,y)=x, область D ограничена прямой, проходящей через точки А(2;0), В(0;2), и дугой окружности с центром в точке С(0;1) радиуса 1, расположенной выше этой прямой.
252.  a=const >0; D –часть круга радиуса а с центром в точке О(0;0), лежащая в первой четверти.
a=const >0; D –часть круга радиуса а с центром в точке О(0;0), лежащая в первой четверти.
253.  D задана вершинами О(0;0), А(1;-1) и В(1;1).
D задана вершинами О(0;0), А(1;-1) и В(1;1).
254. f(x,y)= 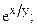 D: y2=x, x=0, y=1.
D: y2=x, x=0, y=1.
255. f(x,y)=  D: y=
D: y=  y=x.
y=x.
256. f(x,y)=  D: x2+y2=1.
D: x2+y2=1.
В задачах 257  259 расставить пределы интегрирования в полярных координатах.
259 расставить пределы интегрирования в полярных координатах.
257.  258.
258. 
 259.
259. 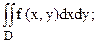 D: y=x, y= –x, y=1.
D: y=x, y= –x, y=1.
260. Вычислить  где D – верхний полукруг, образованный окружностью диаметром а и с центром в точке С(
где D – верхний полукруг, образованный окружностью диаметром а и с центром в точке С( 0) и осью абсцисс.
0) и осью абсцисс.
261. Вычислить  где D: х2+у2=2ах, а>0.
где D: х2+у2=2ах, а>0.
В задачах 262, 263 построить область интегрирования D, площадь которой выражается заданным интегралом.
262.  263.
263.  a>0.
a>0.
В задачах 264  268 вычислить площади заданных областей интегрирования D.
268 вычислить площади заданных областей интегрирования D.
264. D: x=y, x=2y, x+y=a, x+3y=a, где a>0.
265. D: y=0, y2=4ax, x+y=3a (y ³ 0).
266. D: y2=10x+25, y2=-6x+9.
267. D: x2+y2=2x, x2+y2=4x, y=x, y=0.
268. D:  r=2 (x ³ 1).
r=2 (x ³ 1).
269. Построить и вычислить объем тела, заданного своими вершинами: О(0;0;0), А(1;0;0), В(1;1;0), С(0;0;1).
270. Вычислить  где V: 0 £ x £ 1, 0 £ y £ x, 0 £ z £ xy.
где V: 0 £ x £ 1, 0 £ y £ x, 0 £ z £ xy.
271. Найти массу тела, ограниченного поверхностями х2+у2 + z2=16 (х ³ 0, у ³ 0,
z ³ 0) и 2х+3у=6, если его плотность в каждой точке (х; у; z) равна аппликате этой точки.
В задачах 272  277 вычислить интегралы.
277 вычислить интегралы.
272.  273.
273. 
274.  275.
275.  D: 1 £ x £ 2, 0 £ y £ 2.
D: 1 £ x £ 2, 0 £ y £ 2.
276.  D: y=x2, x=y2. 277.
D: y=x2, x=y2. 277.  D: x=2+sin y; x=0, y=0, y=2p.
D: x=2+sin y; x=0, y=0, y=2p.
В задачах 278,279 расставить пределы интегрирования при переходе от двойного интеграла к повторному двумя способами для области интегрирования D.
278. D: x=0, x=1, y=1, 
279. D: 4–угольник АВСD, где A(1;2), B(2;4), C(2;7), D(1;5).
В задачах 280  282 изменить порядок интегрирования.
282 изменить порядок интегрирования.
280.  281.
281.  282.
282. 
В задачах 283  285 вычислить заданный интеграл.
285 вычислить заданный интеграл.
283. 
284. 
285. 
286. Вычислить объем прямого бруса, ограниченного сверху поверхностью z=4-x2-y2 и имеющего основанием квадрат, ограниченный в плоскости Оху прямыми, получающимися при пересечении с плоскостью Оху плоскостей х=±1, у=±1.
287. Вычислить объем тела, ограниченного поверхностями: z=0; 2-x-y-2z=0; y=x2; y=x.
288. Оси двух круговых цилиндров с одинаковыми поперечными сечениями пересекаются под прямым углом. Вычислить объем общей части этих цилиндров.
В задачах 289  298 вычислить объем тела, ограниченного заданными поверхностями.
298 вычислить объем тела, ограниченного заданными поверхностями.
289. x2+y2=4x; z=x; z=2x. 290. z=0; y+z=2; y=x2.
291. y=0; y=3-x2-z2. 292. x2+y2=4x; x2+y2+z2=16.
293. y=1+x2; z=3x; y=5; z=0 (x ³ 0, y ³ 0, z ³ 0).
294. x=1; y=x; y=3x; z=0; z=x2+y2.
295. y=x2; y=1; x+y+z=4; z=0.
296. z=y2-x2; z=0; y=2 (x ³ 0, y ³ 0, z ³ 0).
297. z=4- x2-y2; 2z=2+ x2+y2.
298. x2+y2+z2=R2; z=a; z=b (R>b>a>0).
299. Вычислить площадь поверхности шара.
300. Вычислить площадь части поверхности z2=4x, лежащей в первом октанте, вырезанной поверхностями у2=4x и х=1.
301. Вычислить площадь части поверхности 2у=х2+z2, вырезанной поверхностью х2+z2=1.
302. Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а, считая, что прямоугольник лежит в плоскости хОу.
303. Найти статический момент однородного полукруга, лежащего в плоскости хОу, радиуса R, относительно диаметра.
304. Найти координаты центра масс однородной пластинки, ограниченной в плоскости zОу линиями: ау=z2 и у=2 (а>0).
В задачах 305  310 вычислить объем тела, ограниченного заданными поверхностями.
310 вычислить объем тела, ограниченного заданными поверхностями.
305. z=4–y2; z = y2 +2; x = –1; x = 2.
306. x = 6 – z2 – y2; x2 = y2 + z2 (x  0).
0).
307. x + y +z = 4; x = 3; y = 2; x = 0; z = 0.
308. x2 + y2 +z2 = 2z; x2 + y2 = z2.
309. 2z = x2 + y2; y + z = 4.
310. x2 = 2y; y + z = 1; 2y + z = 2.
В задачах 311,312 вычислить объем пространственной области, заданной системой неравенств.
311. 
312. 
В задачах 313  355 найти объем тела, ограниченного заданными поверхностями.
355 найти объем тела, ограниченного заданными поверхностями.
313. 
314. 
315. 
316. 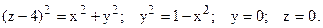
317. 
318. 
319. 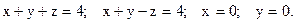
320. 
321. 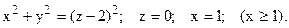
322. 
323. 
324. 
325. 
326. 
327. 
328. 
329. 
330. 
331. 
332. 
333. 
334. 
335. 
336. 
337. 
338. 
339. 
(внутри цилиндров). 

340. 
341.  (вне цилиндра).
(вне цилиндра).
342. 
343. 
344. 
345. 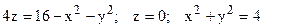 (вне цилиндра).
(вне цилиндра).
346. 
(внутри цилиндров).
347. 
348. 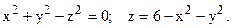
349. 
350. 
351. 
352. 
353. 
354. 
355. 
В задачах 356 ¸ 359 вычислить указанный интеграл по заданной области.
356. 

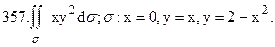

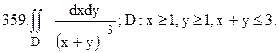
360. Вычислить объем тела, ограниченного поверхностями 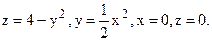
В задачах 361 ¸ 362 вычислить указанный интеграл, перейдя к полярным координатам.


363. Найти объем тела, вырезанного из шара радиуса R прямым круговым цилиндром диаметра R, образующая которого проходит через центр шара.
В задачах 364 ¸ 368 сделать чертеж области интегрирования и изменить порядок интегрирования.





В задачах 369 ¸ 373 перейти от двойного интеграла  к повторному двумя способами; сделать чертеж области D.
к повторному двумя способами; сделать чертеж области D.





В задачах 374¸ 377 найти массу пластины, ограниченной заданными кривыми и имеющей заданную плотность m. Сделать чертеж.
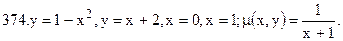

(при вычислении двойного интеграла перейти к полярным координатам).

 (при вычислении двойного интеграла перейти к полярным координатам).
(при вычислении двойного интеграла перейти к полярным координатам).
378. Найти площадь части поверхности  вырезанной
вырезанной
поверхностями 
379. Найти площадь части поверхности  вырезанной поверхностями
вырезанной поверхностями  (при вычислении интеграла перейти к полярным координатам; сделать чертеж).
(при вычислении интеграла перейти к полярным координатам; сделать чертеж).
380. Найти площадь части поверхности  вырезанной поверхностями
вырезанной поверхностями 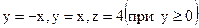 . Cделать чертеж.
. Cделать чертеж.
В задачах 381 ¸383 с помощью двойного интеграла вычислить объем тела, заданного неравенствами. Сделать чертеж.
 (при вычислении интеграла перейти к полярным координатам).
(при вычислении интеграла перейти к полярным координатам).

 (при вычислении интеграла перейти к полярным координатам).
(при вычислении интеграла перейти к полярным координатам).
В задачах 384 ¸ 393 найти массу тела, заданного неравенствами и имеющего заданную плотность m. Сделать чертеж.
 (при вычислении интеграла перейти к
(при вычислении интеграла перейти к
цилиндрическим координатам).

 (при вычислении интеграла перейти к цилиндрическим координатам).
(при вычислении интеграла перейти к цилиндрическим координатам).

 (при вычислении интеграла перейти к цилиндрическим координатам).
(при вычислении интеграла перейти к цилиндрическим координатам).

 (при вычислении интеграла перейти к цилиндрическим координатам).
(при вычислении интеграла перейти к цилиндрическим координатам).

 (при вычислении интеграла перейти к цилиндрическим координатам).
(при вычислении интеграла перейти к цилиндрическим координатам).
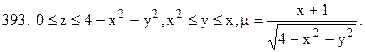
В задачах 394 ¸ 403 изменить порядок интегрирования в повторном интеграле. Сделать чертеж области интегрирования.










В задачах 404 ¸ 413 найти площади плоских фигур, ограниченных заданными кривыми.




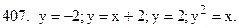






 Представить
Представить  через повторный двумя способами, если
через повторный двумя способами, если 
 Вычислить
Вычислить 
 С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями:
С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями: 
 Вычислить тройной интеграл от
Вычислить тройной интеграл от 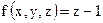 по телу, ограниченному поверхностями:
по телу, ограниченному поверхностями: 
В задачах 418 ¸ 527 вычислить заданный интеграл.

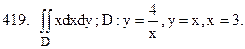






Перейти к полярной системе координат.
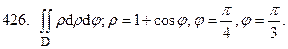

Перейти к полярной системе координат.


Перейти к полярной системе координат.



Перейти к цилиндрической системе координат.

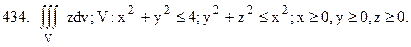


Перейти к сферической системе координат.


Перейти к цилиндрической системе координат.

Перейти к сферической системе координат.
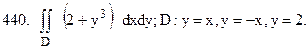




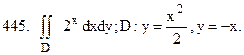


Перейти к полярной системе координат.


Перейти к полярной системе координат.
 .
.
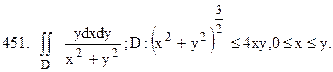



Перейти к цилиндрической системе координат.
 .
.
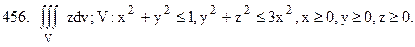


Перейти к сферической системе координат.

Date: 2016-07-22; view: 928; Нарушение авторских прав