
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В. Приложения к механике.
|
|
Приложения тройных интегралов к механике проистекают из задач, связанных с непрерывным распределением массы в пространственной области.
Пусть Т – область пространства, занимаемая каким-либо материальным телом с плотностью m(x, y, z). Тогда
а) 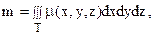 (15)
(15)
где m – масса этого тела;
б) моменты инерции Ix, Iy, Iz относительно координатных осей Ox, Oy, Oz; Ixy, Ixz, Iyz относительно координатных плоскостей xOy, xOz, yOz; I0 относительно начала координат, соответственно, определяются по формулам:
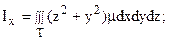
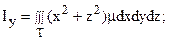
|
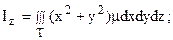
|
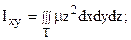
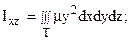
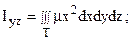
|
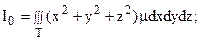
в) координаты центра тяжести тела находятся по формулам:
|
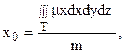
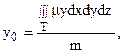
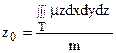
Для однородного тела (m = const) эти формулы упрощаются, т.к. в этом случае можно считать, что m = 1.
Пример 10.
Найти массу и момент инерции относительно оси Oz однородного тела Т, ограниченного поверхностями: z = 4-x2-y2 и 4-2z = x2 + y2.
Тройной интеграл, как было указано выше, позволяет вычислить обе указанные характеристики, если известна объемная плотность тела m(x, y, z):
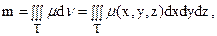
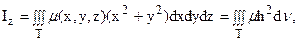
где h = h (x,y,z) – расстояние от текущей точки до оси, относительно которой вычисляется момент инерции, в нашем случае это ось Oz, т.е. h2 = x2 + y2.
В случае однородного тела m(x, y, z) = const = m, и тогда:
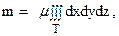
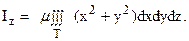
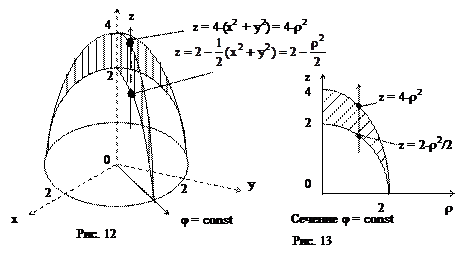
Для вычисления указанных тройных интегралов в данной задаче удобно воспользоваться цилиндрическими координатами. Уравнения данных поверхностей в цилиндрической системе имеют вид: z = 4-r2 и 4-2z = r2. Решая их совместно, получим, что эти поверхности пересекаются по окружности x2 + y2 = 4, z = 0, или в цилиндрической системе координат: r = 2, z = 0.
Итак, данное тело ограничено двумя параболоидами вращения, которые пересекаются по окружности радиуса 2, лежащей в плоскости Oxy (рис. 12).
Ясно, что j меняется от 0 до 2p. При каждом фиксированном j величина r меняется от 0 до 2, а при фиксированных r и j величина z меняется от 2-1/2r2 до 4-r2 (см. рис. 13). Таким образом, имеем:
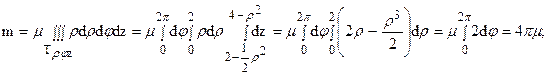
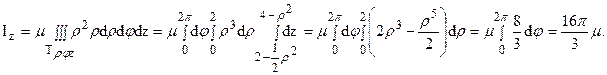
Ответ: m = 4pm(кг); 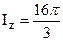 (кгм2).
(кгм2).
Пример 11.
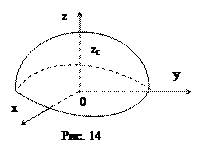 Найти расположение центра масс однородного полушара Т. Выберем прямоугольную систему координат с началом в центре шара так, как указано на рис. 14. Ясно, что абсцисса и ордината центра масс
Найти расположение центра масс однородного полушара Т. Выберем прямоугольную систему координат с началом в центре шара так, как указано на рис. 14. Ясно, что абсцисса и ордината центра масс
xc = yc = 0.
Для нахождения zc воспользуемся известной формулой: 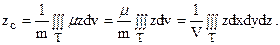 В предпоследнем равенстве использована однородность тела, а в последнем – определение объемной плотности однородного тела. Хотя объем тела v можно вычислить с помощью тройного интеграла, но в нашем случае имеется «школьная» формула V
В предпоследнем равенстве использована однородность тела, а в последнем – определение объемной плотности однородного тела. Хотя объем тела v можно вычислить с помощью тройного интеграла, но в нашем случае имеется «школьная» формула V 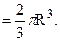 Оставшийся тройной интеграл вычислим в сферических координатах:
Оставшийся тройной интеграл вычислим в сферических координатах:
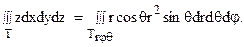
Так как в рассматриваемом случае 0 < j < 2p, 0 < q < p/2, 0 < r < R, то
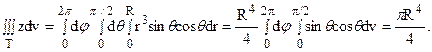
Ответ: xc = yc = 0, zc = (8/3)R.
Пример 12. (см. пример 2 стр. 183)
Найти массу тела с плотностью m = x + y + z, ограниченного плоскостями
x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.
Тело, массу которого необходимо найти, является прямоугольным параллелепипедом. Согласно формуле (15) имеем:
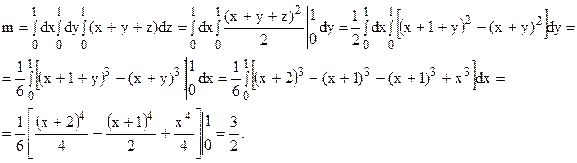
Пример 13.
Найти моменты инерции однородного (m = 1) цилиндра с высотой «h» и радиусом основания «а» относительно диаметра основания и относительно оси цилиндра, считая, что ось цилиндра направлена по оси Ох.
Поместим начало координат в центр нижнего основания цилиндра. Тогда уравнение цилиндра будет иметь вид y2 + z2 = a2. Моменты инерции, которые мы находим, будут равны моментам инерции относительно координатных осей Oz и Ox. Следовательно, имеем:
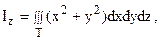
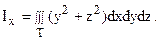
Введем цилиндрические координаты: y = rcosj, z = rsinj, x = x, и тогда
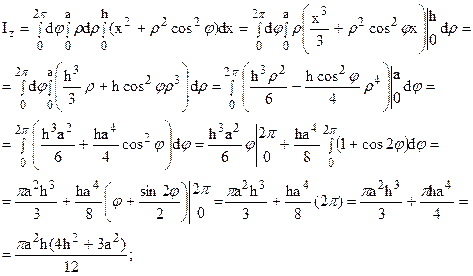
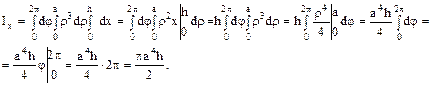 |
Пример 14.
|
x + y + z = 1, x = 0, y = 0, z = 0 (см. рис. 15). Согласно формулам (17) имеем:
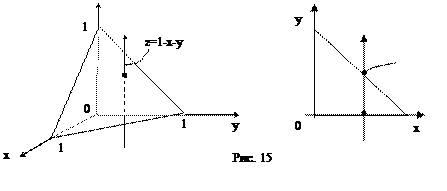
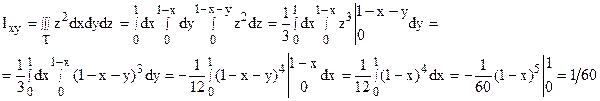
Пример 15.
Вычислить момент  инерции однородного шара (m=1) радиуса
инерции однородного шара (m=1) радиуса  1 относительно его центра. Поместим начало координат в центр шара. Тогда момент инерции шара относительно центра будет равен моменту инерции шара относительно начала координат. Согласно формуле (18) имеем:
1 относительно его центра. Поместим начало координат в центр шара. Тогда момент инерции шара относительно центра будет равен моменту инерции шара относительно начала координат. Согласно формуле (18) имеем:
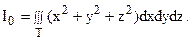
Введя сферические координаты, получим:
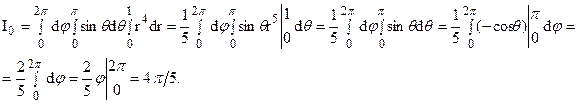
Пример 16.
Найти координаты центра тяжести однородного тела, ограниченного параболоидом 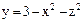 и плоскостью у = 0 (у
и плоскостью у = 0 (у  0).
0).
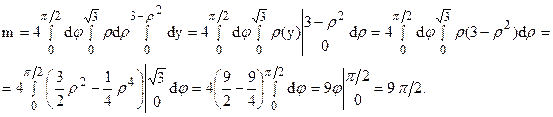 |
В силу симметрии тела относительно координатных плоскостей уОz и хОу (см. рис. 22 §1) x0 = z0 = 0. Для нахождения y0 найдем массу тела m. Введем цилиндрические координаты:
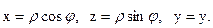
Согласно формулам (15), (19) имеем:
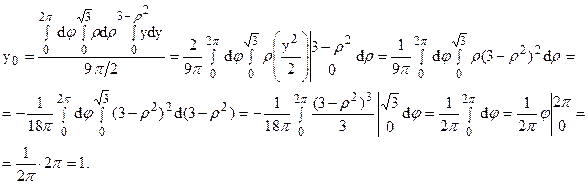
Date: 2016-07-22; view: 906; Нарушение авторских прав