Приложения тройного интеграла.

А. Вычисление объемов.

(см. первое свойство тройного интеграла)

В цилиндрических и сферических координатах соответственно имеем:

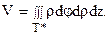(13) (14)

Пример 7.

Вычислить объем тела, ограниченного поверхностями: z = x² + y², x = 0, y = 0, z = 1, z = 2 и расположенного в первом октанте.

Для вычисления тройного интеграла, задающего объем данного тела, воспользуемся цилиндрическими координатами:

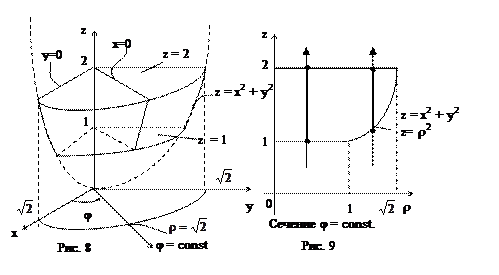Отметим, что z = x² + y² – параболоид вращения, сечение которого плоскостями z = const – окружности, имеющие радиус . Поэтому данное тело имеет указанный на рис. 8 вид. Для точек тела угол j меняется в пределах от 0 до p/2. При каждом фиксированном j r меняется от 0 до – радиуса верхнего основания тела (рис. 9). Так как нижняя граница изменения z задается по-разному на разных участках: при 0 < r < 1, 1 < z < 2, а при 1 < r < , x² + y² = r² < z < 2 то интеграл разобьется на два:

Пример 8.

Вычислить объем тела, ограниченного цилиндрами z = 4-y² и z = y² + 2 и плоскостями x = -1, x = 2.

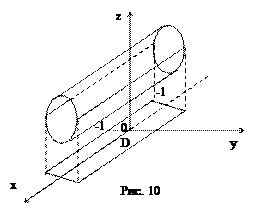Тело, объем которого находим (рис. 10), ограничено снизу цилиндром z = y² + 2, а сверху – цилиндром
z = 4-y².

Оно проектируется в область D плоскости xOy, ограниченную прямыми x = -1, x = 2, y = 1 и y = -1.

С учетом симметрии области V относительно плоскости xOz, имеем:

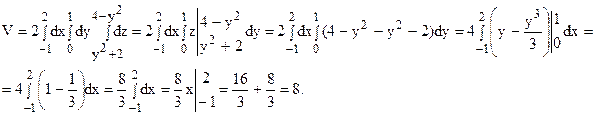
Пример 9.

Вычислить объем тела, ограниченного параболоидом x = 6-z²-y² и конусом
x² = y² + z² (x > 0).

y = rcosj, z = rsinj, x = x.

С учетом того, что данное тело симметрично относительно плоскостей xOz и xOy и что уравнения окружности, ограничивающей область D, конуса и параболоида, соответственно, принимают вид r = 2, x = r и х = 6-r², имеем:

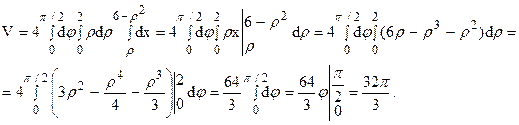
Date: 2016-07-22; view: 627; Нарушение авторских прав