Вычисление тройных интегралов в криволинейных координатах.

Как и в случае двойных интегралов, тройной интеграл часто удобно вычислять в криволинейных системах координат. Мы рассмотрим лишь цилиндрические и сферические координаты.

В общем же случае, как и для двойных интегралов, это производится через якобиан преобразования, в котором добавляются частные производные для третьей координаты.

Введем цилиндрическую систему координат Orjz, у которой полюс совпадает с началом координат О прямоугольной декартовой системы координат Oxyz, полярная ось r совпадает с полуосью Ox, а угол φ отсчитывается от полярной оси против часовой стрелки.

Будем считать, что 0 < r < +¥, 0 < j < 2p, -¥ < z < +¥.

Выпишем формулы, выражающие декартовы координаты точки через цилиндрические– они очевидны из рассмотрения рис. 5: x = rcosj, y = rsinj, z = z. (8)

Эти формулы показывают, что введение цилиндрических координат фактически сводится к введению полярных координат на плоскости Oxy, поэтому переход в тройном интеграле к цилиндрическим координатам может быть осуществлен следующим образом:

(9)

где D_rj – та же проекция D_xy тела Т на Oxy, но рассматриваемая в полярных координатах.

Для цилиндрических координат якобиан

.

Введем сферическую систему координат Orjq (см. рис. 5), у которой полюс совпадает с началом системы координат Oxyz, долгота j отсчитывается от оси Ox в направлении против движения часовой стрелки, а широта q – от оси Oz, r - расстояние точки М от полюса, причем, 0 < r < +¥, 0 < j < 2p, 0 < q < p. Выпишем формулы, выражающие декартовы координаты точки через сферические (см. рис. 5):

Тогда, поскольку здесь ½J½= r²sinq формула перехода в тройном интеграле от декартовых к сферическим координатам будет иметь вид:

(11)

Вопрос о переходе к той или иной системе координат зависит от вида подынтегральной функции и области интегрирования.

Пример 5.

Вычислить тройной интеграл , если область Т ограничена плоскостью y = 2 и параболоидом x² + z² = 2y.

Введем цилиндрические координаты:

x = rcosj, z = rsinj, y = y.

Так как x² + z² = r²cos²j + r²sin²j = r², то

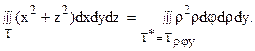
В области Т* координата j меняется от 0 до 2p, r – от 0 до 2, y – от параболоида r²/2 до плоскости y = 2.

И тогда

Пример 6.

Вычислить тройной интеграл , если область Т ограничена сферой x² + y² + z² = z.

Date: 2016-07-22; view: 652; Нарушение авторских прав