D. Приложения двойного интеграла к механике.

Пусть D – плоская пластинка, лежащая в плоскости xOy, с поверхностной плотностью массы m(x, y).

Тогда:

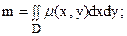
б) статические моменты M_x и M_y пластинки относительно координатных осей OX и Oy находят по формулам:

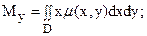(19) (20)

в) координаты центра тяжести x_c и y_c пластинки – по формулам:

x_c = M_y/m (21) y_c =M_x/m; (22)

г) моменты инерции I_x, I_y и I_o пластинки соответственно относительно координатных осей Ox, Oy и начала координат находят по формулам:

(23) (24)

Для однородных пластинок m = const и для простоты мы в этом случае будем считать m = 1.

Пример 27.

Вычислить момент инерции относительно начала координат плоской однородной пластины, ограниченной линиями: y = 2/x, y = 2, y = -2, x = 4, x = -4. Момент инерции плоской пластины относительно точки О может быть вычислен, если известна плотность этой пластины:

где m – плотность в «текущей» точке М;

d – расстояние от М до полюса О. В декартовой системе координат, если О – начало координат, то:

причем, последнее равенство справедливо в предположении, что пластина однородна, т.е. m = const.

Так как в данной задаче область симметрична относительно начала координат, и, кроме того, f(-x, -y) = f(x, y), то, обозначив через D_*, например, верхнюю половину области D и разделив ее на две правильные области прямой x = 1, получим (рис.29).

Ответ:

Пример 28.

Найти статический момент однородного прямоугольника со сторонами a и b относительно стороны а, считая, что прямоугольник лежит в плоскости xOy.

Поместим начало координат в одну из вершин прямоугольника, а ось Ox направим по стороне а. Статический момент прямоугольника относительно стороны а будет равен статическому моменту прямоугольника относительно оси Ох. По формуле (19) имеем:

Пример 29.

Найти статический момент однородного полукруга, лежащего в плоскости xOy, радиуса R относительно диаметра.

Поместим начало координат в середину диаметра полукруга, а ось Oy направим по диаметру (рис. 30). Тогда статический момент полукруга относительно диаметра будет равен статическому моменту полукруга относительно оси Oy. С учетом того, что уравнение окружности, ограничивающей полукруг, имеет вид x² + y² = R², а в полярных координатах
r = R, по формуле (18) имеем:

Пример 30.

Найти координаты центра тяжести однородной пластинки, ограниченной параболой ay = z² и прямой y = 2 (a > 0).

Пластинка лежит в плоскости yOz. В силу симметрии пластинки относительно оси Oy имеем z_c = 0. Для нахождения y_c найдем M_z и m:

И тогда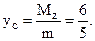

Пример 31.

Найти момент инерции квадрата со стороной а, поверхностная плотность которого пропорциональна z, относительно одной из вершин, считая, что квадрат находится в плоскости xOz.

Поместим начало координат в одну из вершин квадрата, а координатные оси Ox и Oz направим по двум взаимно перпендикулярным его сторонам. Тогда искомый момент инерции будет равен моменту инерции квадрата относительно начала координат, т.е.

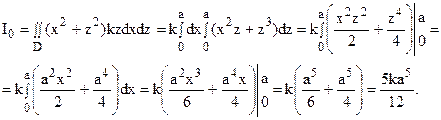
Тройной интеграл

Date: 2016-07-22; view: 826; Нарушение авторских прав