
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение. Вычисление тройных интегралов в декартовых прямоугольных координатах.
|
|
Тройной интеграл представляет собой одно из возможных обобщений двойного интеграла на случай функции трех переменных.
Пусть в пространственной области Т задана функция f(x, y, z). Проделаем 5 операций:
6. Разобьем область Т на n частей DТ1, DТ2,…,DТn, не имеющих между собой общих внутренних точек. Обозначим объемы и диаметры этих частей соответственно черезDv1, Dv2,…, Dvn и l1, l2, …, ln. Наибольший из диаметров обозначим через l и назовем его рангом дробления.
7. Выберем в каждой частичной области DТk(k = 1, 2, …, n) по точке
(xk; yk; zk) и вычислим в ней значение функции f(x, y, z), т.е. найдем числа
f(xk, yk, zk).
8. Вычислим произведения f(xk, yk, zk)×Dvk.
9. Найдем сумму  которую называют интегральной суммой для функции f(x, y, z) в области Т, отвечающей выбранному дроблению на частичные области и выбору точек (xk, yk, zk).
которую называют интегральной суммой для функции f(x, y, z) в области Т, отвечающей выбранному дроблению на частичные области и выбору точек (xk, yk, zk).
10. Измельчая дробление, ищем предел
|
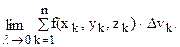
|


При этом функцию f(x, y, z) называют подынтегральной функцией, Т – областью интегрирования, x, y, z – переменными интегрирования, а dv (или dxdydz) – элементом объема.
|
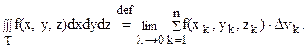
Приведем простейшие свойства тройного интеграла, которые непосредственно следуют из определения его и доказываются аналогично соответствующим свойствам определенного и двойного интегралов.
1. Если в области Т f(x, y, z) º 1, то  где V =VТ – объем области Т.
где V =VТ – объем области Т.
2. Постоянный множитель К в подынтегральной функции можно выносить за знак тройного интеграла:
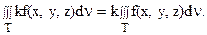
3. Тройной интеграл от суммы двух функций равен сумме тройных интегралов от слагаемых:
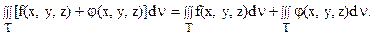
Свойства 2 и 3 выражают свойство линейности тройного интеграла относительно подынтегральной функции.
4. Если область интегрирования Т разбита на две части Т1 и Т2, то

Это свойство называют свойством аддитивности тройного интеграла относительно области интегрирования.
5. Если всюду в области Т функция f(x, y, z) удовлетворяет условию f(x, y, z) > 0, то 
6. Если всюду в области Т функции f(x, y, z) и j(x, y, z) удовлетворяют условию
f(x, y, z) > j(x, y, z), то
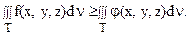
7. Имеет место неравенство:

8. (Теорема о среднем.) Если функция f(x, y, z) непрерывна в замкнутой области Т, то в этой области найдется хотя бы одна такая точка 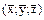 , что будет иметь место равенство:
, что будет иметь место равенство: 
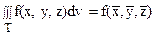 VТ,
VТ,
где V Т – объем области Т.
Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Осуществляется это с помощью следующих теорем.
 Теорема 1
Теорема 1
 Если sху – замкнутая плоская область, являющаяся проекцией на плоскость Oxy замкнутой пространственной области Т, поверхность которой снизу и сверху описывается уравнениями z = h(x,y) и z = H(x,y), где h(x,y) и H(x,y) – непрерывные функции в sx,y, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей является граница области sx,y (рис. 1), то для любой функции f(x,y,z), непрерывной в Т, имеет место формула
Если sху – замкнутая плоская область, являющаяся проекцией на плоскость Oxy замкнутой пространственной области Т, поверхность которой снизу и сверху описывается уравнениями z = h(x,y) и z = H(x,y), где h(x,y) и H(x,y) – непрерывные функции в sx,y, и цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей является граница области sx,y (рис. 1), то для любой функции f(x,y,z), непрерывной в Т, имеет место формула
|
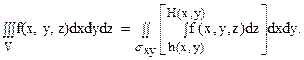 (4)
(4)
Если при этом область sx,y ограничена линиями x = a, x = b, y = j(x), y = y(x), где a < b, а функции j(x) и y(x) непрерывны на промежутке [a, b] и удовлетворяют условию
j(x) < y(x), то, переходя в формуле (4) от двойного интеграла к повторному, получим формулу:
|
 (5)
(5)
При вычислении тройного интеграла по формуле (5) сначала вычисляется внутренний интеграл по переменной z при постоянных x и y, затем полученная функция от х и y интегрируется по переменной y при постоянном х, а затем полученная функция от х интегрируется по х в пределах от а до b.
Если область Т спроектировать не на плоскость Oxy (как в теореме 1), а на Oyz, то получим следующий аналогичный результат.
 Теорема 2
Теорема 2
Если syz – замкнутая плоская область, являющаяся проекцией на плоскость Oyz замкнутой пространственной области Т, поверхность которой сзади и спереди описывается уравнениями x = h(y,z) и x = H(y,z), где h(y,z) и H(y,z) – непрерывные функции в syz, и цилиндрической поверхностью, у которой образующая параллельна оси Oх, а направляющей является граница области syz, то для любой функции f(x,y,z), непрерывной в Т, имеет место формула:
|
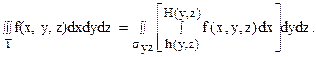
Если при этом область syz ограничена линиями y = с, y = d, z = j(у), z = y(у), где c < d, а функции j(y) и y(y) непрерывны на промежутке [c, d] и удовлетворяют условию
j(x) < y(x), то, переходя в формуле (6) от двойного интеграла к повторному, получим формулу:
|
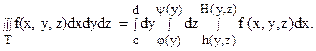
При вычислении тройного интеграла по формуле (7) сначала вычисляется внутренний интеграл по переменной x при постоянных y и z, затем полученная функция от y и z интегрируется по переменной z при постоянном y, а затем полученная функция от y интегрируется по y в пределах от c до d.
Если область T спроектировать на плоскость Oxz, то можно получить теорему 3, аналогичную теоремам 1 и 2.
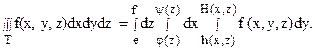
Выражения, стоящие в правых частях равенств (5) и (7), называют повторными (трехкратными) интегралами.
Заметим, что пределы интегрирования будут постоянными во всех трех интегралах только в том случае, если областью интегрирования является параллелепипед с гранями, параллельными координатным осям.
Если область интегрирования T имеет более сложный вид, то ее следует разбить на конечное число частей, каждая из которых удовлетворяет условиям одной из указанных теорем. Интеграл по области при этом заменяется суммой интегралов по ее частям.
При вычислении тройных интегралов основную трудность обычно составляет (как, впрочем, и для двойных) расстановка пределов интегрирования при переходе к повторным (трехкратным) интегралам.
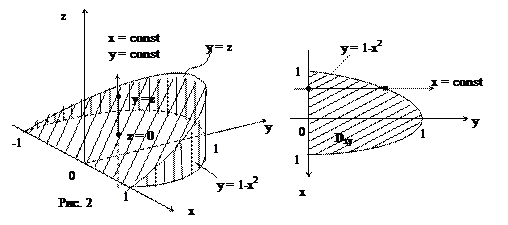
Пример 1.
Вычислить тройной интеграл 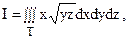 если тело ограничено поверхностями: y = 1-x2, y = z, y = 0, z = 0 (рис. 2).
если тело ограничено поверхностями: y = 1-x2, y = z, y = 0, z = 0 (рис. 2).
Тело Т, ограниченное тремя плоскостями y = z, y = 0, z = 0 и параболическим цилиндром y = 1-x2, является, как нетрудно видеть, правильным в направлении параллельном оси Oz, т.е. всякая вертикальная прямая, проходящая через внутренние точки тела, пересекает его границу в двух точках.
При этом, прямая x = const, y = const входит в тело при z = 0, а выходит при z = y.
В таком случае интеграл можно записать в виде (4):
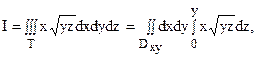
где Dxy – проекция тела на плоскость Oxy. Так как эта проекция, в свою очередь, является правильной в направлении оси Oy, то искомый интеграл можно записать в виде трехкратного типа (5):
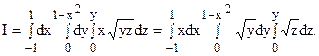
Последовательно вычисляя интегралы, получим:
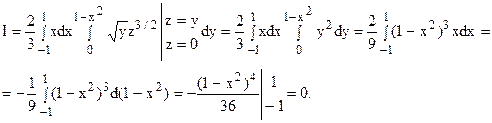
Ответ: I = 0.
Пример 2.
 Вычислить тройной интеграл
Вычислить тройной интеграл  по области Т, ограниченной плоскостями x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.
по области Т, ограниченной плоскостями x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.
Вычисляем данный интеграл по формуле (5):

Внутренний интеграл вычисляем, считая x и у постоянными:
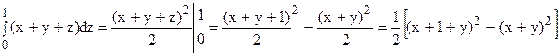
Полученную функцию от х и у интегрируем по у, считая х постоянным:
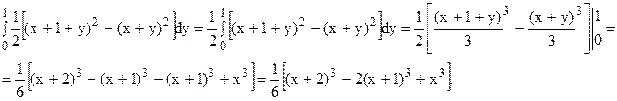
Полученную функцию от х интегрируем по х:
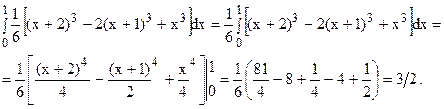
Обычно для сокращения записи все вычисления записывают в одну строку следующим образом:
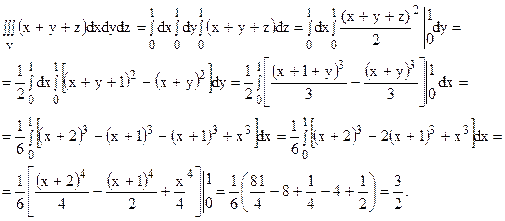
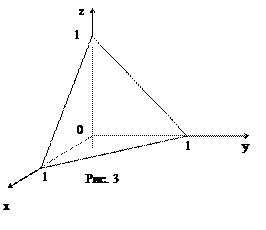 Пример 3.
Пример 3.
Вычислить тройной интеграл  если область Т ограничена плоскостями x = 0, y = 0, z = 0 и
если область Т ограничена плоскостями x = 0, y = 0, z = 0 и
z = 1-x-y.
В этой задаче область Т можно спроектировать, например, на плоскость yOz. Тогда область Т (рис. 3) имеет нижнюю границу x = 0 и верхнюю границу x = 1-y-z. Область Dyz проектируется в отрезок [0; 1] оси Oy и имеет границы z = 0 и z = 1-y. Переходя к повторному интегрированию, получим:
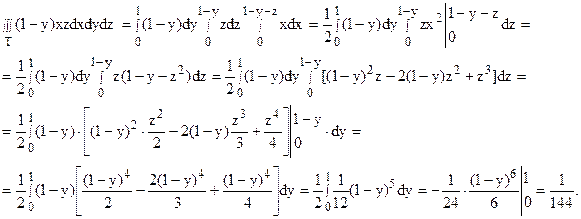
Пример 4.
Вычислить тройной интеграл  , если область Т ограничена плоскостями:
, если область Т ограничена плоскостями:
x = 1, y = 0, z = 0, x + y + z = 2.
Изобразим область Т (рис. 4).

Выберем порядок следования переменных интегрирования такой: x, y, z, т.е. пирамиду ADEF спроектируем на плоскость Oxy. В этом случае х меняется от 1 до 2. Уравнение прямой AD имеет вид y = 0, а уравнение прямой АЕ получается, если в уравнении x + y + z = 2 плоскости ABC положить z = 0.
Итак, прямая АЕ имеет уравнение y = 2-x. Уравнение плоскости ADE имеет вид z = 0, а уравнение плоскости AEF известно. Если его разрешить относительно z, то получим z = 2-x-y. Теперь в согласии с формулой (5) можем написать:

Date: 2016-07-22; view: 985; Нарушение авторских прав