Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
C. Вычисление площади поверхности
|
|
Пусть поверхность s, заданная уравнением z = f(x, y), проектируется на плоскость xOy в область D (см. рис. 1). Тогда ее площадь S находят по формуле:
|
Пример 24.
Найти часть поверхности параболоида вращения z = x2 +y2, вырезанной плоскостями x = 0, y = 0 и z = 2 (x ³ 0, y ³ 0).
|
| |||
| |||
где D – проекция рассматриваемой части поверхности на плоскость Оху.
В данной задаче D есть четверть круга, изображенная на рис. 25,26. Так как по условию задачи z = x2 +y2, то z’x = 2x, z’y = 2y и 1 + (z’x)2 + (z’y)2 = 1 + 4(x2 + y2).
Введя полярные координаты, получим:
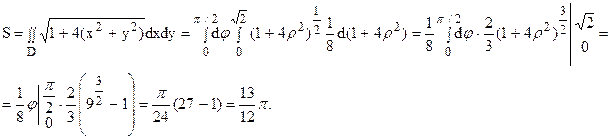
Пример 25.
Вычислить площадь части поверхности цилиндра z2 = 4x, лежащей в I октанте, вырезанной цилиндром y2 = 4x и плоскостью x = 1.
Из урав нения поверхности z2 = 4x для первого октанта имеем:
и 
Область D (рис. 27) есть параболический сегмент, ограниченный в плоскости xOy параболой y2 = 4x, или 
и прямой x = 1. Тогда
|
х=1
0 1 х
Пример 26.
Вычислить площадь части поверхности параболоида 2y = x2 + z2, вырезанной цилиндром x2 + z2 =1.
В этой задаче поверхность однозначно проектируется только на плоскость xOz. Поэтому ее площадь будем вычислять по формуле:
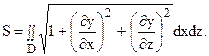
Из уравнения параболоида находим:
|
откуда 
Date: 2016-07-22; view: 2167; Нарушение авторских прав