В. Вычисление объемов.

Объем цилиндрического тела, ограниченного сверху поверхностью
z = f(x, y), а снизу – областью D плоскости xOy (рис. 21), находится по формуле (см. геометрический смысл двойного интеграла):

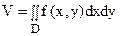Если тело не является цилиндрическим, то его разбивают на цилиндрические части.

Пример 20.

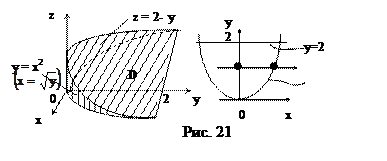Вычислить объем тела, ограниченного плоскостями z = 0,
y + z = 2 и цилиндром y = x².

Данное тело (рис. 21) сверху ограничено плоскостью z = 2 – y, поэтому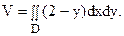

Область D есть параболический сегмент, ограниченный в плоскости xOy прямой y = 2 и параболой y = x². Спроектируем область D на ось Oy. Тогда, с учетом симметрии тела относительно плоскости yOz, получим:

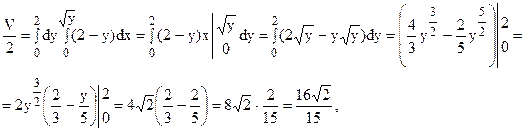
откуда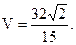

Пример 21.

Вычислить объем тела, ограниченного плоскостью y = 0 и параболоидом
y = 3 – x² – z².

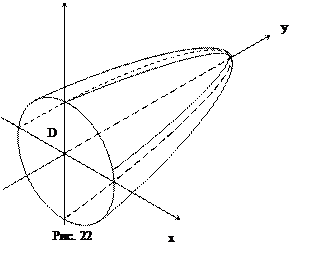В этой задаче удобно считать, что тело «стоит» на плоскости xOz и «сверху» (рис. 22) ограничено параболоидом y = 3 – x² – z², поэтому

	z
		О

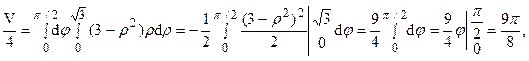
откуда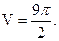

Пример 22.

Вычислить объем тела, вырезанного цилиндром x² + y² = Rx из сферы
x² +y² + z² = R².

На рис. 23 изображена половина тела, объем которого мы и найдем (вторая половина, расположенная симметрично с первой, находится под плоскостью xOy).

	D

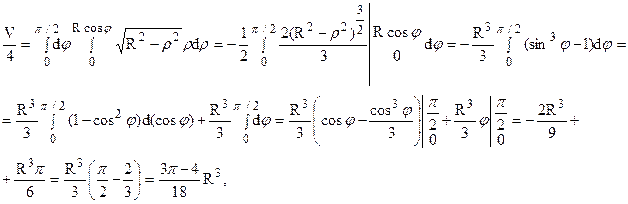откуда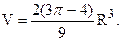

Пример 23.

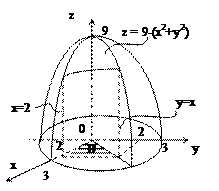
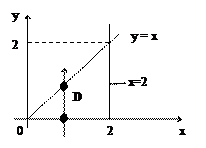Найти объем тела, ограниченного поверхностями: x² + y² = 9 – z, y = x, x = 2, y = 0, z=0.

Заданное тело является цилиндроидом, так как это – часть некоторого цилиндра, ограниченная снизу плоскостью z = 0, а сверху – поверхностью z = 9 - x² - y² (рис. 24). Объем цилиндроида, ограниченного сверху поверхностью z = f(x, y), можно вычислить с помощью двойного интеграла по области, лежащей в его основании (рис. 1):

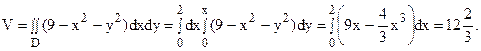
Date: 2016-07-22; view: 3008; Нарушение авторских прав