
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.
|
|
|
u = u(x,y), v = v(x,y) –
|
x = x(u,v), y = y(u,v).
Тогда каждой точке М(x;y) из области Dxy будет взаимно однозначно соответствовать пара чисел (u,v), называемых криволинейными координатами этой точки. Если область Dxy расположена в той части плоскости xOy, в которой введены криволинейные координаты u, v, то справедлива следующая формула:
|
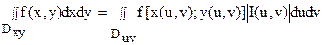 ,
,
где Duv – область изменения криволинейных координат u и v, отвечающая области Dxy, а I(u,v) – якобиан преобразования (8):
|
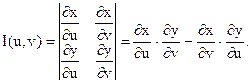
Например, для полярных координат имеем:
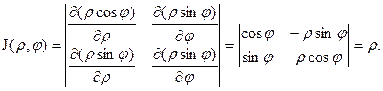
В зависимости от строения области интегрирования или подынтегральной функции вычисление двойного интеграла может оказаться более простым не в прямоугольной, а в какой-нибудь из криволинейных систем координат. Наиболее распространенной из них является полярная.
Для того, чтобы преобразовать двойной интеграл в прямоугольных декартовых координатах в двойной интеграл в полярных координатах, нужно x и y в подынтегральной функции заменить соответственно через rcosj и rsinj, а выражение dxdy заменить выражением rdrdj:
|
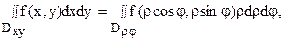
где Drj – та же область Dху, но описанная в полярных координатах (поскольку в этом случае якобиан I = r).
В этой формуле следует обратить внимание на то, что в подынтегральной функции не только происходит замена координат по формулам перехода от декартовых к полярным, но и появляется дополнительный множитель r.
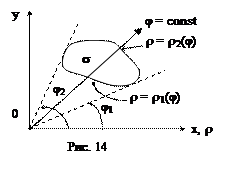 Вычисление двойного интеграла в полярной системе координат, также как и в декартовой, сводится к двукратному интегрированию, но, соответственно, по переменным r и j. Расстановку пределов при вычислении интегралов в полярных координатах можно производить, используя чертеж области интегрирования на плоскости Oxy и геометрический смысл полярных координат.
Вычисление двойного интеграла в полярной системе координат, также как и в декартовой, сводится к двукратному интегрированию, но, соответственно, по переменным r и j. Расстановку пределов при вычислении интегралов в полярных координатах можно производить, используя чертеж области интегрирования на плоскости Oxy и геометрический смысл полярных координат.
Пусть, например, внешнее интегрирование производится по j и область Dρφ является правильной в направлении j = сonst, т.е. каждый луч, выходящий из начала координат, пересекает область Dρφ по отрезку
(рис. 14).
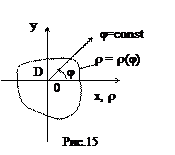 Тогда справедлива формула:
Тогда справедлива формула:
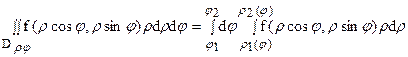 (12)
(12)
В частном случае, когда D содержит начало координат, имеем:
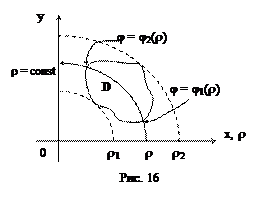
|
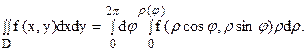
Если же внешнее интегрирование производится по r и область Dρφ является правильной в направлении
r = const, т.е. каждая окружность пересекает, имея центром начало координат, область Dρφ по дуге этой окружности (только в двух точках) (см. рис.16), то справедлива формула:
|
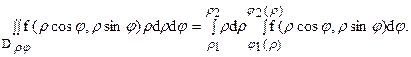
Пример 12.
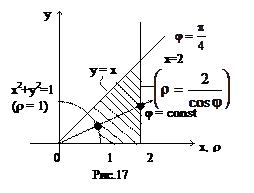 Вычислить двойной интеграл
Вычислить двойной интеграл 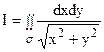 по области, ограниченной линиями: x2 + y2 = 1, y = 0, x = 2, y = x и лежащей в первом квадранте.
по области, ограниченной линиями: x2 + y2 = 1, y = 0, x = 2, y = x и лежащей в первом квадранте.
Хотя данный интеграл можно вычислить в прямоугольной декартовой системе координат, в которой он задан, но неопределенные интегралы, которые при этом возникнут, достаточно сложны.
Перейдем к полярной системе координат. Вспомним, что 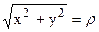 . Построив область интегрирования (рис. 17), мы видим, что для точек области полярный угол меняется в пределах от 0 до p/4, а при каждом значении j из этого промежутка полярный радиус меняется от 1 до 2/cosj (последнее мы получим, подставив в уравнение х = 2 выражение для х через полярные координаты: rcosj = 2 и разрешив полученное соотношение относительно r).
. Построив область интегрирования (рис. 17), мы видим, что для точек области полярный угол меняется в пределах от 0 до p/4, а при каждом значении j из этого промежутка полярный радиус меняется от 1 до 2/cosj (последнее мы получим, подставив в уравнение х = 2 выражение для х через полярные координаты: rcosj = 2 и разрешив полученное соотношение относительно r).
Таким образом, искомый интеграл можно представить в виде:
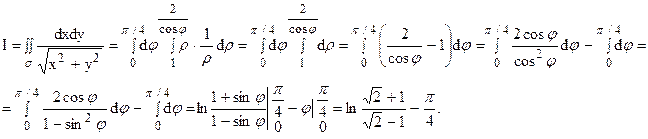
Пример 13. 
Вычислить двойной интеграл 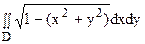 , если область D ограничена окружностью x2 + y2 = 1.
, если область D ограничена окружностью x2 + y2 = 1.
Область D есть круг радиуса 1 с центром в начале координат. Введем полярные координаты. В полярных координатах x2 + y2 = r2 и уравнение окружности принимает вид r = 1.
Тогда по формуле (13) получаем:
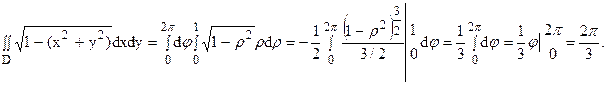
Пример 14.
Вычислить двойной интеграл 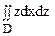 , если область D ограничена половиной дуги окружности x2 + z2 = ax и отрезком оси Ox от точки с абсциссой равной 0 до точки с абсциссой равной а.
, если область D ограничена половиной дуги окружности x2 + z2 = ax и отрезком оси Ox от точки с абсциссой равной 0 до точки с абсциссой равной а.
Область D – полукруг. Введем полярные координаты: x = rcosj, z = rsinj.
Уравнение окружности в полярных координатах принимает вид r2 = racosj, или r = acosj.
Подынтегральная функция имеет вид z = rsinj. Угол j меняется от 0 до p/2 (полукруг находится в I четверти). При каждом фиксированном значении угла j r меняется от 0 (в начале координат) до r = acosj (на окружности). Тогда получаем:

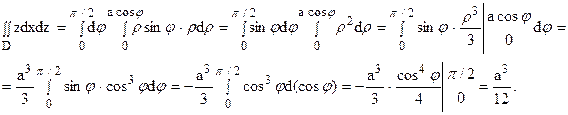
Пример 15.
 В двойном интеграле
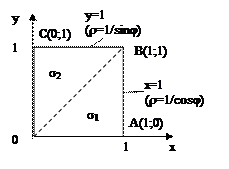
В двойном интеграле 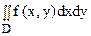 расставить пределы интегрирования в полярных координатах, если область D является квадратом с вершинами в точках О(0;0), А(1;0), В(1;1), С(0;1).
расставить пределы интегрирования в полярных координатах, если область D является квадратом с вершинами в точках О(0;0), А(1;0), В(1;1), С(0;1).
Уравнение стороны АВ (х = 1) в полярных координатах принимает вид rcosj = 1, или r = 1/cosj, а ВС будет r = 1/sinj. Угол j меняется от 0 до p/2 (квадрат находится в I четверти). При изменении угла от 0 до p/4 r меняется от 0 до r = 1/cosj, а при изменении угла от p/4 до p/2 r меняется от 0до r = 1/sinj.
Следовательно,
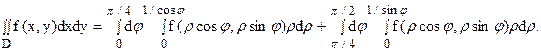
Пример 16.
Вычислить двойной интеграл 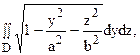 если область D ограничена эллипсом
если область D ограничена эллипсом 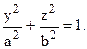
Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив y = arcosj, z = brsinj.
Найдем якобиан данного преобразования:
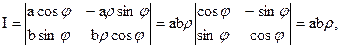 т.е. | I |= abr.
т.е. | I |= abr.
Подынтегральная функция принимает вид:
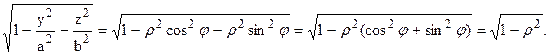
Теперь имеем:
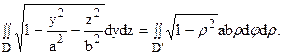
Угол j меняется от 0 до 2p. Уравнение эллипса принимает вид r = 1, поэтому r меняется от 0 до 1. И тогда

Date: 2016-07-22; view: 1515; Нарушение авторских прав