Перемена порядка интегрирования.

Если область s является простой как вида 1), так и вида 2), то применимы обе формулы (5) и (6), следовательно,

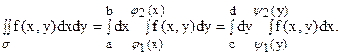
Иными словами, повторное интегрирование не зависит от порядка интегрирования. Этим обстоятельством часто пользуются при вычислении двойного интеграла, выбирая ту из двух формул, которая приводит к более простым выкладкам.

В качестве упражнения на расстановку пределов интегрирования полезна задача о перемене порядка интегрирования в повторном интеграле

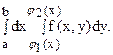
Прежде всего, следует начертить область интегрирования s, которая находится в полосе между прямыми x = a и x = b и ограничена снизу линией
y = j₁(x), а сверху – линией y = j₂(x). Затем область s проектируют на ось Oy и находят уравнения прямых y = c и y = d, ограничивающих снизу и сверху полосу, в которой расположена область s; затем находят левую границу области s х = j₁(y) и правую x = j₂(y). Если какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область s приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Аналогично, если требуется переменить порядок интегрирования в повторном интеграле

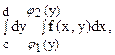
то, спроектировав область s на ось Ox, находят уравнения прямых x = a и x = b, нижнюю границу области s y = j₁(x) и верхнюю y = j₂(x).

Иногда область s приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Пример 7.

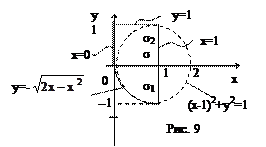В двойном интеграле расставить пределы для одного и другого порядка интегрирования по области s, ограниченной прямыми x =0, x = 1, y = 1 и кривой Область s (рис. 9) находится в полосе между прямыми x = 0 и x = 1. Нижняя граница – дуга окружности 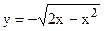, верхняя – прямая y = 1. Следовательно,

Область s проектируется на ось Oy в отрезок [-1,1]. Левая граница области имеет уравнение 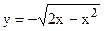, т.е. при –1 £ y £ 0 и x = 0 при 0 £ y £ 1. Правая граница x = 1. Разбивая область на две части s₁ и s₂, а интеграл - на сумму двух интегралов, получим:

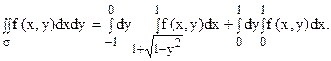
Пример 8.

В двойном интеграле расставить пределы для того и другого порядка интегрирования по области s, которая является параллелограммом с вершинами в точках А(1;2), В(2;4), С(2;7), D(1;5).

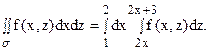
Для того, чтобы расставить пределы в другом порядке, разбиваем область s на три части (см. рис. 10):

и тогда получим:

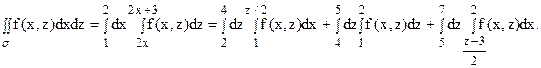
Пример 9.

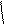z=y

Поэтому область s следует разбить на две части (s₁ и s₂), а интеграл – на сумму интегралов: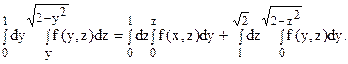

Пример 10.

В двойном интеграле расставить двумя способами пределы интегрирования по области s, определенной неравенствами: , y +1 ³ 0, -1 £ x £ 3.

		Область интегрирования s, ограниченная верхней ветвью параболы y2 = x + 1, горизонтальной прямой y = -1 и двумя вертикальными прямыми x = -1 и x = 3, изображена на рис. 12. В первом случае внутренний интеграл берется при условии x = const. Прямая x = const при входе в область s пересекает прямую y =-1, а при выходе из s – параболу , поэтому (см.формулу (5)):

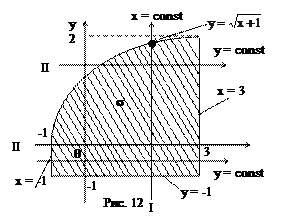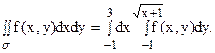
Во втором случае переменная y принимает значения –1 £ y £ 2 (координаты точки пересечения параболы и прямой x = 3 будут x = 3; ). Внутренний интеграл вычисляется при условии y = const. Прямая y = const при выходе из области s пересекает прямую x = 3, а при входе – либо прямую x = -1 (если –1 £ y < 0), либо параболу x=y²–1 (если 0 £ y £ 2), т.е. левая граница состоит из двух различных кривых. Таким образом, область s разбивается на две части: s₁ и s₂ прямой y = 0, а интеграл представляется в виде суммы двух интегралов:

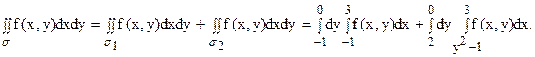
Пример 11.

Из записи интеграла видно, что область интегрирования разбита на 3 области: первая ограничена линиями: x = -2, x = 0, y = -2, y = 2; вторая – линиями: x = 0, x = 4, y = -2, y = - ; третья – линиями: x = 0, x = 4, y = , y = 2 (рис. 13).

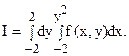
Date: 2016-07-22; view: 691; Нарушение авторских прав