
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение и вычисление двойных интегралов в декартовых прямоугольных координатах.
|
|
Двойной интеграл представляет собой одно из возможных обобщений определенного интеграла на случай функции двух переменных. Дадим ему определение.
Пусть в плоской области s задана функция f(x, y). Проделаем 5 операций:
1. Разобьем область s на n частей Ds1, Ds2,…,D sn, не имеющих между собой общих внутренних точек. Обозначим площади и диаметры этих частей соответственно через DS1, DS2,…, DSn и l1, l2, …, ln. Наибольший из диаметров обозначим через l и назовем ее рангом дробления, т. е. 
2. Выберем в каждой ячейке Dsk(k = 1, 2, …, n) произвольно по точке
(xk; yk) и вычислим в них значения функции f(x, y), т.е. найдем числа f(xk, yk).
3. Вычислим произведения f(xk, yk)×DSk(k = 1, 2, …, n).
4.
|

которую называют интегральной суммой для функции f(x, y) в области s, отвечающей данному дроблению и выбору точек (xk, yk).
5. Измельчая дробление, ищем предел для (1), т.е.
|

Если существует конечный предел (2), не зависящий ни от способа дробления области s на части, ни от выбора точек (x1, y1), (x2, y2),…, (xn, yn), то этот предел называют двойным интегралом от функции f(x, y) по области s и обозначают символами:
 или
или 
При этом функцию f(x, y) называют подынтегральной функцией, s – областью интегрирования, x, y – переменными интегрирования, а ds (или dxdy) – элементом площади.
Таким образом, по определению:
|

Аналогичные построения двойного интеграла имеют место и тогда, когда область s лежит либо в плоскости xOz, либо в плоскости yOz. Например, если область s лежит в плоскости xOz, то получаем 
Учитывая, что z = f(x, y) в пространстве определяет некоторую поверхность, проекция которой на плоскость xOy дает область s, видим, что выражение f(xk, yk)×DSk дает объем цилиндра, основание которого есть DSk, а высота равна f(xk, yk). Интегральная сумма равна сумме n объемов таких цилиндров. В пределе она дает объем тела, ограниченного сверху поверхностью z = f(x, y), снизу – областью s, а с боков – цилиндрической поверхностью, направляющая которой – граница области s, а образующая – прямая, параллельная оси Oz. В этом и состоит геометрический смысл двойного интеграла.
 |
(*)
Перечислим простейшие свойства двойного интеграла, которые непосредственно следуют из его определения и доказываются аналогично соответствующим свойствам для определенного интеграла.
1. Если f(x,y) = 1 всюду в области s, то  где S означает площадь области s.
где S означает площадь области s.
2. Постоянный множитель k подынтегральной функции можно выносить за знак двойного интеграла:
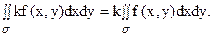
3. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от слагаемых:

Свойства 2 и 3 выражают свойство линейности двойного интеграла относительно подынтегральной функции.
4. Если область интегрирования s разбита на две части s1 и s2, то есть
s = s 1+ s2, то

Это свойство называют свойством аддитивности двойного интеграла относительно области интегрирования.
5. Если всюду в области s функция f(x,y) удовлетворяет условию f(x, y)³0, то 
6. Если всюду в области s функции f(x, y) и j(x, y) удовлетворяют условию f(x, y) £ j(x, y), то 
7. Имеет место неравенство:

8. (Теорема о среднем.) Если функция f(x, y) непрерывна в замкнутой области s, то в этой области найдется хотя бы одна такая точка  что будет иметь место равенство:
что будет иметь место равенство:
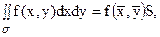
где S означает площадь области s.
Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Имеют место теоремы.
 Теорема 1.
Теорема 1.
Если функция f(x, y) непрерывна в замкнутой области s, ограниченной линиями x = a, x = b, y = j(x), y = y(x) (здесь a < b, а функции j(x)и y(x) непрерывны на промежутке [a, b] и удовлетворяют условию j(x) £ y(x)), то имеет место равенство:
|

Выражение, стоящее в правой части равенства (4), называется повторным (двукратным) интегралом от функции f(x, y) по области s, причем, пределы внешнего интеграла постоянны, а внутреннего – переменные (пределы внутреннего интеграла будут постоянны лишь в том случае, когда область s является прямоугольником со сторонами, параллельными осям координат).
Повторный интеграл, стоящий в правой части равенства (4), обычно записывают в виде:
|


При вычислении двойного интеграла с помощью формулы (4) сначала вычисляется внутренний интеграл по переменной y

 при постоянном значении переменной x, а затем полученная функция от х интегрируется по х в пределах от а до b.
при постоянном значении переменной x, а затем полученная функция от х интегрируется по х в пределах от а до b.
| |||
 | |||
 | |||
Рис.2
 Теорема 2.
Теорема 2.
Если функция f(x, y) непрерывна в замкнутой области s, ограниченной линиями y = c, y = d, x = f(y), x = y(y) (здесь c >d, а функции f(y) и y(y) непрерывны на промежутке [c,d] и удовлетворяют условию f(y) £ y(y)), то имеет место равенство:
|




 При вычислении двойного интеграла с помощью формулы (6) сначала вычисляется внутренний интеграл
При вычислении двойного интеграла с помощью формулы (6) сначала вычисляется внутренний интеграл  при постоянном значении переменной y, а затем полученная функция от y интегрируется по y в пределах от c до d.
при постоянном значении переменной y, а затем полученная функция от y интегрируется по y в пределах от c до d.
 При этом предполагается, что область s является правильной (простой) в направлении y = const (оси Ox), т.е. всякая прямая y = const, проходящая через внутренние точки области, пересекает границу этой области ровно в двух точках, причем, f(y) и y(y) – ординаты, соответственно, точки входа прямой в область и точки выхода из нее (рис. 3).
При этом предполагается, что область s является правильной (простой) в направлении y = const (оси Ox), т.е. всякая прямая y = const, проходящая через внутренние точки области, пересекает границу этой области ровно в двух точках, причем, f(y) и y(y) – ординаты, соответственно, точки входа прямой в область и точки выхода из нее (рис. 3).
Если область интегрирования s имеет более сложный вид, то ее следует разбить на конечное число частей, каждая из которых удовлетворяет условиям теоремы 1 или 2. Интеграл по области s заменяется при этом суммой интегралов по ее частям.
Заметим в заключение, что прежде чем решить вопрос об использовании либо формулы (5), либо (6), следует изобразить область s графически и выбрать, какая из переменных x или y будет внешней переменной интегрирования, а какая внутренней.
Пример 1.
 Вычислить двойной интеграл
Вычислить двойной интеграл  по прямоугольной области s, ограниченной прямыми x = 1, x = 2, y = 0, y = 2.
по прямоугольной области s, ограниченной прямыми x = 1, x = 2, y = 0, y = 2.
 Вычисляем данный интеграл по формуле (5):
Вычисляем данный интеграл по формуле (5):


Внутренний интеграл вычисляем, считая x постоянным (т. е. по у):

Полученную функцию от х интегрируем по отрезку [1, 2] по переменной х:

Обычно вычисления внутреннего интеграла отдельно не делают, а все выкладки записывают в одну строку следующим образом:


Такой записью мы и будем пользоваться в дальнейшем.
Пример 2.
| |||
 | |||
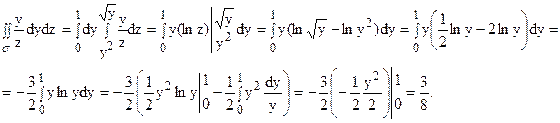 Интеграл
Интеграл  взят методом интегрирования по частям, причем при подстановке нижнего предела использован тот факт, что
взят методом интегрирования по частям, причем при подстановке нижнего предела использован тот факт, что 
Пример 3.
|

 Вычислить двойной интеграл
Вычислить двойной интеграл 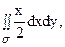 если область s ограничена кривой x = 2 + siny и прямыми x= 0, y = 0, y = 2p.
если область s ограничена кривой x = 2 + siny и прямыми x= 0, y = 0, y = 2p. 


 Область s (рис. 5) является простой относительно оси Oy. Левая ее граница x = 0, а правая x = 2+siny. При любом фиксированном значении y из отрезка [0, 2p] x меняется от x = 0 до x = 2 + siny, поэтому по формуле (6) имеем:
Область s (рис. 5) является простой относительно оси Oy. Левая ее граница x = 0, а правая x = 2+siny. При любом фиксированном значении y из отрезка [0, 2p] x меняется от x = 0 до x = 2 + siny, поэтому по формуле (6) имеем:

Пример 4.

Вычислить интеграл  , если область s ограничена линиями y = (x– 1)2 и y = x + 1.
, если область s ограничена линиями y = (x– 1)2 и y = x + 1.
|
|
|

Напомним, что при вычислении внутреннего интеграла «внешняя» переменная х считается постоянной:

Интегрируя теперь по «внешней» переменной и применяя для упрощения вычислений замены t = x + 1 и t = x – 1 в интегралах, получим:

Пример 5.


 Вычислить двойной интеграл
Вычислить двойной интеграл  если область s ограничена прямой y = x + 3 и параболой y = x2 + 1.
если область s ограничена прямой y = x + 3 и параболой y = x2 + 1.
|
 Изобразим вначале область s (рис. 7). В этом примере разумно воспользоваться формулой (5), т.е. внешнее интегрирование проводить по х, а внутреннее – по y.
Изобразим вначале область s (рис. 7). В этом примере разумно воспользоваться формулой (5), т.е. внешнее интегрирование проводить по х, а внутреннее – по y.
|

|

Пример 6.
Вычислить интеграл  по области s, ограниченной линиями y = - x, y = 1, y = x2 (рис. 8).
по области s, ограниченной линиями y = - x, y = 1, y = x2 (рис. 8).
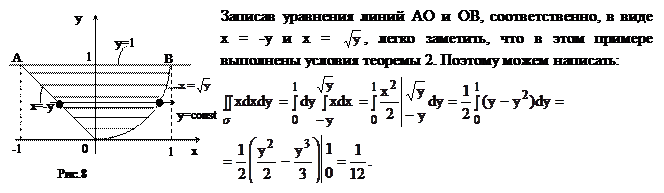
Date: 2016-07-22; view: 921; Нарушение авторских прав
 если область s ограничена параболами z = y2 и y = z2.
Область
если область s ограничена параболами z = y2 и y = z2.
Область  (перед радикалом ставим только знак «+», т.к. область s находится в той части области плоскости yOz, где z > 0).
При любом фиксированном значении y из отрезка [0, 1] z меняется от z = y2 до
(перед радикалом ставим только знак «+», т.к. область s находится в той части области плоскости yOz, где z > 0).
При любом фиксированном значении y из отрезка [0, 1] z меняется от z = y2 до