Полиномы над полем R

Т.к. R сод-т С, то мн-н f(x) м/о рассмотреть как мн-н над полем С. Над полем С f(x) м/о разложить в произведение n линейных мн-лей, где n=N(f(x)).

…

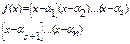-действит. корни, - мнимые корни.

М/т оказаться, что все корни действительные или мнимые.

Т 1: Мнимые корни мн-в с действит. коэф-ми попарно сопряжены, т.е.

если и x₀ кореньf(x), то корень f(x).

Док-во: Пусть x₀ корень f(x), т.е. =. Покажем, что число сопряж-е с x₀, тоже корень f(x)

ч.т.д.

Т 2: Кратности сопряж-х корней в мн-нах с дейст-ми коэф-ми

одинаковы, т.е. если k

кратность x₀, то - также

имеет кратность k.

Доказ-во: Пусть x₀ имеет кратность k, а сопряж-й ему корень имеет кратность s, тогда ; т.к. , то по св-м простых мн-в , где

Допустим, что 1) k>s, тогда .

Рассм-м произ-е:

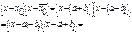. ,т.к. a,bÎR

Тогда

и т. к. , то получаем, что . Но тогда должен иметь корень . Но он его не имеет, т. к. . След-но, случай k>s невозможен.

2) Аналогично док-ся невоз-ть случая k<s.

Следствие 1: Кол-во мнимых корней у мн-на с действ. коэф-ми всегда четное.

Следствие 2: Если мн-н с действ. коэф-ми имеет нечетную степень, то он имеет хотя бы один действ. корень.

По опр-ю мн-н ненулевой степени над полем P наз-ся неприводимым, если он м/б разложен в произ-е мн-в над этим же полем, степень которых >0, но меньше степени f(x).

Следствие: Над полем дейст-х

чисел люб. мн-н степени ³ 3

приводим. Это следует из след.

теоремы.

Т: Люб. мн-н ненулевой степени ³ 3 с действ. коэф-ми разлагается над полем R в произв-е мн-в 1-й и 2-й степени.

Доказ-во: f(x)Î R[x] Над полем

комплексных чисел

,

где -действит. корни, - мнимые корни.

Первые S мн-й остав-т без изменения, а мн-ли с мнимыми числами перем-т попарно со своими сопряженными, получая при этом мн-н второй степени с дейтв. коэф-ми.

Следствие:

Если N(f(x))>1, то

1. при N(f(x))=2 мн-н м/б как приводим, так и неприводим

Пр: - приводим

- неприводим

2. N(f(x))>=3-приводим всегда