Метрические пространства

ОПР: метрическим простр-м наз. произвольное мн-во X в кот. каждой паре элементов поставлено в соответствие неотриц. действ. число , (называемое расст-м от x до y), удовлетв-е следующим условиям:

1 ,т. и т.т. к. x=y (аксиома тождества).

2. Для любых эл-в (аксиома симметрии).

3. Для любых эл-в (аксиома треугольника).

ПР: 1.Евклидово n-мерное простр-во его эл-ми явл. упорядоченные наборы из n действ. чисел , , ,

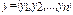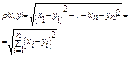м/о док-ть, что 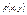удовл-т всем условиям. Частный случай:

а)R - мн-во действ. чисел

б) R²-пл-ть, его эл-ты пары , , тогда

,

в) R³- трехмерное прост-во.

2. Гильбертово прост-во l₂, его эл-ми явл. посл-ти действ. чисел 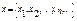, такие, что - сх-ся.

,

3. Прост-во непрер-х ф-ций с[a,b], его точками явл. ф-ции x=x(t) непр-е на [a,b]

Полное метр-е прост-во

Пусть дано метр-е прост-во X с метрикой p(x,y).

ОПР: Послед-ть x(n) точек метр-го пр-ва X наз. фундамен-й, если("e>0)($N)("m,n)(m>N,n>NÞr(x_m,x_n)<e), т. е. p(x,y)®0, при m,n®¥ (по мере увеличения номеров послед-ти, рас-е м/у чл-ми посл-ти умен-ся).

Т: Если посл-ть x(n) сх-ся, то она фунд-на.

Док-во: Пусть x(n) сх-ся в т. x это озн-т по опр-ю ("e>0)($N)("n)(n>NÞr(x_n,x)<e¤ 2) ("m)(m>NÞr(x_m,x)<e¤ 2), тогда r(x_m,x_n)£ (по нер-ву тр-ка) r(x_n,x)+r(x_m,x)<e¤ 2+e¤ 2=e, т.е. посл-ть фунд-ная.

Фунд-ть есть необх-е усл-е сх-ти, м/о док-ть, что в пр-ве R это усл-е явл-ся и дост-ным. Это формул-ся в крит-и Каши. Но это спр-во не для любого метр-го пр-ва R.

ОПР: Метр-е пр-во E наз полным, если в нем каждая фунд-я посл-ть сх-ся к т. пр-ва из E.

Критерий Каши: Для того, чтобы посл-ть x(n) точек полного метр-го пр- ва X сх-сь необ-мо и дост-но, чтобы она была фунд-й, но в полном пр-ве.

Необх-ть сл-ет из теоремы, а дост-ть сл-ет из опр-я полноты прост-ва.

Зам: Очевидно, что мн-во E замкнутое (оно сод-т все свои пред-е точки)мн-во пол-го метр-го пр-ва X, то E само явл-ся полным метр-м прост-вом.

P.S. Т.x₀ÎX наз. предельной точкой мн-ва E если в люб. ее окрест-ти сущ-т точка мн-ва отлич-я от x₀.

Пр: 1. Пр-во R полное, что сл-ет из критерия Каши.

2. Rⁿ-полное, это сл-ет из полноты пр-ва R, т. к. сх-ть посл-ти из Rⁿ свод-ся к сход-ти n- посл-ти коор-т.

3. Пр-во C [a,b] полное, его эл-ми явл-ся все непр-е на [a,b] ф-ции.

4. l₂ - полное пр-во.