Понятие о вероятности

Вероятность события. Статистическое определение вероятности.

Мы часто сравниваем события, говоря что одно из них более вероятно, чем другое. В связи с этим, чтобы придать данному сравнению точный кон. смысл, требуется с каждым событием связать некоторое число, кот. выражало бы степень возможности события, т.е. было бы тем больше, чем более возможное событие. Это число мы назовем вероятностью. Вероятностью события наз-ся кол-ная мера степени объективной возможности данного события. Пусть произведено n испытаний, в результате которых событие А появилось m раз. Относительной частотой (частностью) события А наз-ся отношение числа m появления события к общему числу n всех испытаний 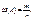Статистич. определение: при большом числе испытаний относительная частота большинства событий изменяется мало, колеблясь около некоторого постоянного числа р. Это число р и называют вероятностью события А. Н-р: При бросании монеты частота выпадения герба колеблется около Ѕ. Вероятность показывает как часто в среднем появляется событие А. Н-р: р=2/7 говорит о том, что при большом числе испытаний событие появляется в среднем в 2 случаях из 7.

Классическое определение вероятности.

Событие А и В называют несовместными, если появление одного из них исключает появление другого в одном и том же испытании. A*B=V. Событие А₁,А₂, …, А_n образуют полную группу, если в результате испытания обязательно произойдет хотя бы одно из них, т.е. А₁+А₂+…+А_n = достоверно. События наз-ют равновозможными, если нет ни каких объективных причин, для того, чтобы одно из них появилось чаще, чем другое. Пусть события А₁,А₂, …, А_n образуют полную группу равновозможных попарно несовместных событий. Такие события наз-ют элементарными исходами. Прим: кубик, А1-четное число, А2 - нечетное. Предпочтительнее в качестве элементарных исходов выбирать такие, чтобы любое событие, связанное с данным опытом распадалось на них, т.е. было представимо в виде суммы некоторых из них. Т.е. элементарные исходы при которых появлялось событие А, т.е. которые в сумме составят А наз-ют благоприятствующими событию А. Вероятностью события А наз-ют отношение числа m исходов благоприятствующих событию А к общему числу n всех элементарных исходов. Р(А) = m/n.

. Свойства вероятностей.

1⁰ Вероятность любого события А удовлетворяет неравенству 0£P(A)£1. Док-во: 0£m£n; (: n) 0£(m\n)£1. 2⁰ Вероятность достоверного события равно 1. Очевидно что все исходы благоприятствуют событию, т.е. m=n. 3⁰ Вероятность невозможного события = 0. т. к. событие невозможно, ни один из исходов не благоприятствуют, т.е. m = 0. Формула полной вероятности.

Пусть событие А может произойти с одним и только с одним из попарно несовместных событий В₁, В₂,…,В_n, образующих полную группу. Т.к. заранее не известно какое из событий В_i произойдет, то их наз-ют гипотезами, очевидно что наступление события А равносильно наступлению одного из попарно несовместных событий АВ₁ или АВ₂ или... АВ_n, т.е. А=АВ₁+АВ₂+…+АВ_n. По теореме сложения для несовместных событий имеем: Р(А)=Р(АВ₁)+Р(АВ₂)+…+Р(АВ_n), по теореме умножения имеем: Р(А)=Р(В₁)*Р_В1(А)+Р(В2)*Р_В2(А)+…+Р(В_n)*Р_Вn(А). P(A)=∑P(B_K)*P_BK(A)