Преобразование подобия в плоскости

О1: Подобием с коэф-ом k>0 наз. произведение гомотетии с этим же коэф -ом и произвольным центром на движение j= H₀^kg.

j - подобие, H₀^k- гомотетия, g – движение.

Св-ва: 1⁰. При подобии с коэф-ом k все расстояния умножаются на k. H₀^k: M®M^/, N®N^/, êM^/N^/ ê=kúMNú Þ êM^//N^// ê= kúMNú

g: M^/®M^//, N^/®N^//, êM^//N^// ê=úM^/N^/ú

2⁰. H₀^k=1 = e, j=eg=g, т.е. движение – частный случай подобия.

g=e, j= H₀^ke=H₀^k – гомотетия – частн. случай подобия.

3⁰. Если при преобразовании j: M®M^/, N®N^/ и выполняется рав-во êM^/N^/ ê =kúMNú, то j - подобие с коэф. k.

êM^*N^* ê =kúMNú Þ f₁: M®M^*, N®N^*Þ f₁=H₀^k- гомотетия.

êM^/N^/ ê =úM^*N^*ú Þ f₂: M^*®M^/, N^*®N^/ Þ f₂=g – движение.

f₁f₂= H₀^kg=j - подобие.

О2: Подобием с коэф. k называют такое преобразование пл-ти, при кот. расстояние м/у двумя точками умножается на k.

4⁰. Подобие м/о предст-ть в виде произведения движения на гомотетию с произвольным центром и с коэф-м.

j - подобие с коэф-м Þ j= H₀^kg (на основании О2).

g: M®M^*, N®N^*, êM^*N^* ê =úMNú,

H₀^k: M^*®M^/, N^*®N^/, êM^/N^/ ê=kúMNú,сл-но gH₀^k: M®M^/, N®N^/; так что вып. рав-во êM^/N^/ ê=kúMNú Þ на основ. О2 Þ gH₀^k – подобие.

Гомотетия – частн. вид подобия.

О: Гомотетия с данным центром О и коэф. kÎR, k¹0 наз. такое отображение плоскости на себя, при кот. вып. рав-во для любой т.М и её образа М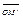^/, = k .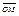

k>0 – прямая гомотетия, k<0 – обратная гомотетия.

При k=1 = .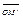

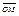Аналитическое выражение: x^/=kx,

y^/=ky.

Задание гомотетии: 1) М/о задать центром и коэфф-м; 2) Парой соотв-щих точек (M,M^/) и (N,N^/) так, чтобы MN êêM^/N^/,а прямые MM^/ и N не êê.

3) Гомот-я м.б. задана центром О, т.А, т.А^/; О, А, А^/ должны лежать на одной прямой.

4) Гомот-я м.б. задана аналитически с пом. Формул, выражающих коор-ты образа ч/з прообраз.

Св-ва гомотетии:

1. При гомот. с коэф-м k все расстояния умн-ся на êk ê.

H₀^k: M®M^/, N®N^/ Þ êM^/N^/ ê=

= êk êúMNú.

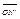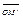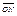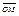= - = k 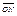- 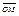k = k( - ) =k ,

= k Þ M^/N^/ êêMN и

êM^/N^/ ê=êk êêMNê.

2. При гомот. прямая преобр-ся в паралл-ю ей прямую.

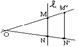
H₀^k: (MN) ® (M^/N^/) и M^/N^/ êêMN, т.к. векторы паралл-ны.

3. Прямая, прох-щая ч/з центр гомотетии, преобразуется в себя.

(MN) прох. ч/з т.О Þ (M^/N^/)=(MN).

4. При гомот. сохраняется деление отрезков в данном отношении.

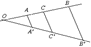
Док-ть: ,

Док-во: .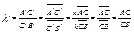

1. При гомот. отрезок преобраз. в отрезок, луч в луч.

H₀^k: [AB]={AB, M: M/AB}®{A^/, B^/, M^//A^/B^/}=[ A^/B^/].

2. Паралл-е прямые преобр-ся в паралл-е прямые (паралл-сть прямых при гомотетии сохр-ся).

l₁ // l₂ Þ .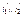

Т: Множество всех гомотетий с одним и тем же центром образует группу относительно операции композиции преобразований.

Для док-ва этой теоремы дост-но проверить 2 треб-ния, к-рым должна удовл-ть указанная операция, т.к. мн-во всех преобразований образует группу, сл-но дост-но проверить треб-ние лишь д/подгруппы.

О: Оп-ция на данном мн-ве д.б. выполнимой, т.е. композиция гомотетий с одним центром явл-ся гомотетией с тем же центром.

О: Преобраз-е, обратное гомотетии явл-ся гомотетией с тем же центром(Сущ-ние нейтрализующего эл-та).

О: Подобием с коэф-ом k>0 наз. произведение гомотетии с этим же коэф-м и произвольным центром на движение.

j=Н₀^k g (j - подобие, Н₀^k- гомотетия, g –движение).

Группа подобий и её подгруппа.

Мн-во всех подобий образует группу.

1) j₁- подобие с коэф. k₁, j₂- подобие с коэф. k₂.

Док-ть: j_1°j₂- подобие.

Док-во: Т.к. подпбие с коэф-ом – это такое преобразование пл-ти, при к-ром расст-е м/у любыми 2-мя точками изменяется на k.

j₁: M®M^/, N®N^/ иú M^/N^/ú=k₁ú MNú,

j₂: M^/®M^//, N^/®N^// иú M^//N^//ú=k₂ú M^/N^/ú, сл-но ú M^//N^//ú=k₁k₂ú MNú.

Сл-но композиция j_1°j₂ есть подобие с коэф-ом k₁k₂.

2) Преобраз-е, обратное подобию, явл-ся подобием с коэф-ом, обратным данному коэф-ту.

j: M®M^/, N®N^/ иú M^/N^/ú=kú MNú,

j ^-1: M^/®M, N^/®N иú MNú=(1/k)ú M^/N^/ú, сл-но j ^-1- подобие с коэф-ом 1/k.

В группе подобий подгруппы движений и подгруппы гомотетий с данным центром.

Система

x^/=k(x cosa - ey sina)+x₀,

y^/=k(x sina + ey cosa)+y₀, Это формула подобия.

Date: 2016-02-19; view: 443; Нарушение авторских прав