Особые решения

Т: Если в уравнении y¢=f(x,y) ф-ия f(x,y) и её частная производная 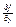непрерывны в некоторой области D, содержащей точку (x₀,y₀), то существует единсвенное решение данного уравнения y=j(x), удовлетворяющее начальному условию y₀=j(x₀).

(в условиях теоремы через каждую точку области D проходит единственная интегральная кривая)

О: Общим решением диф-го ур-ия 1-го порядка наз. ф-ия у=j(x,C), удовл-ая условиям:

1. Она является решением данного ур-ия при "С

2. Для "-го начального условия y(x₀)=y_0, при котором сущ-ет ед-ое решение данного уравнения м. найти такое значение С=С₀, что ф-ия у=j(x,C₀) удовлетворяет данному начальному условию j(x_0,C₀)=y_0.^(n-

Т.о. из общего решения находятся не все решения диф-го Ур-ия, а только такие, которые являются ед-ми, при некоторых начальных условиях. Сущ-ют решения диф-ых Ур-ий, которые не могут быть получены из общего. Это такие, через каждую точку которых проходит более одной интегральной кривой.

О: Решением диф-го ур-ия наз. особым, если через каждую его точку проходит по крайней мере еще одна, касающаяся его интегральная кривая.

Т: Если в уравнении y⁽ⁿ⁾=f(x,y,y¢,y²…y^(n-1)) ф-ия f(x,y) и её частные производные по y,y¢,y²,…,y^(n-1) непрерывны в некоторой области D, содер-ей точку (x₀,y_0,y₀¢,…,y₀^(n-1), то сущ-ет ед-ое решение данного уравнения у=j(x), удовлетворяющее данному начальному условию j(x₀)=y₀, j¢(x₀)=y₀¢,…,j^(n-1)(x₀)=y₀^(n-1).

Аффинные преобразования плоскости.

Пусть на плоскости заданы 2 аффинных репера R и R¢

РИС 2

R(O,e_x,e_y) и R (O¢, e_x¢,e_y¢) тогда отображение М®М¢. Что её координаты в репере R¢ равны соот-но коорд-ам т.М в т.М¢

Опр. Аффинное преобразование- это такое преобразование, при котором М®М¢, а коор-ты x=x^*,y=y^*.

R-старый репер, R¢-новый репер, М(x,y)_R, M¢(x,y)_R¢.

Обозначим М¢(x¢,y¢)_R¢

Дано: О¢(a,b), e_x¢(m₁,n₁),e_y¢(m₂,n₂), e_x¢| | e_y¢Þ

Переход от новой системы координат к старой

x¢=a+m₁x+m₂y

y¢=b+n₁x+n₂y

Это формула аффинного преобразования

Свойства:

1⁰ При аф-ом преобр-ии сохраняется принадлежность точки прямой и непринадлежность

s: Ax+By+Cz=O_R MÎsÞM¢Îs¢

_S¢: Ax+By+Cz=O_R¢ MÏsÞM¢Ïs¢

2⁰ При аффинном преобразовании сохраняется простое отношение трех точек на прямой

3⁰ Параллельные прямые преобразуются в параллельные.

4⁰ Пересекающиеся в пересекающиеся.

5⁰ При аффинном преобразовании отрезок преобрзуется в отрезок, луч в луч.

- Аффинные преобразования определяются вполне тремя парами соот-их точек

(А,А¢), (В,В¢), (С, С¢)

- Множество всех аффинных преобразований образует группу.

Док-во:

1. Произведение 2-х аф-ых преобразований является аф-ым преоб-ем

Рис 3

Координаты т.М² в репере R² будут соот-но равны коор-ам т. М в репере RÞ будут аф-ым.

2. Преобразование обратное аффинному тоже является аф-ым.

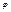-аффинное преобразованиеÞ -аф-ое прео-ие (из определения).

Подгруппы

- множество движений

- множество подобий

Применение к решению задач