Функции комплексного переменного. Теорема Тейлора

,

Это гомотетия с цен. В начале коор-т и коэф-ом подобия с коэф-ом a.

3)

Это парал-ый перенос на вектор b.

2. Дробно-линейная ф-ия , где a,b,c-пост-е компл-ые числа, причем ad×bc¹0, т.к. если ad-dc=0, т.е. a/c=b/d. Обратная ф-ия

так же явл. дробно-лин-й, обл. ф-ции явл-ся однозначной, поэтому дробно-лин-я ф-ция осуществ-ет взаимнооднозначное отображение в расширенной компл-ой пл-ти на себя.

Свойства: 1⁰Круговое(образом любой прямой или окр-ти при дроб.-лин-ом отображении явл. прямая или окр-ть).2⁰Групповое(мн-во всех дробно-лин. ф-ий образует группу)3⁰Сохранение симметрии(2 точки наз. симм-ми относ-но данной прямой или окр-ти, если любая прямая и окр-ть, проходящая через данные точки ортогональны данной прямой или окр-ти)

3.Степенная ф-ия с натур.показателем .Эта Ф-ия яв-ся однозначной или аналитической во всей компл-ой пл-ти

т.к. при z¹0, то отображение с пом. этой ф-ции явл.конфорным во всех z₁¹0

Радикал 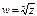-обратная к степенной: .Она явл-ся n-значной, все значения которой можно найти по формуле

4.Показ-ая и тригоном-ая ф-я.

(1)

(2)

(3)

Эти ряды сх-ся по всей компл-ой пл-ти.

Формулы Эйлера: заменим в рав-ве (1) z на iz

Анал-но представив z=-iz в(1) получим

Сложением и вычитанием получили

Возьмем в тригонометр-ой форме y:

Получим показат-ю форму записи комп-го числа

5.Логарифзаяф-ия компл-го числа w=lnz явл-ся обрат-ой ф-ци z=e^w,т.к. e^w¹0, то логар-ая ф-ия определена при люб.z¹0. ,

w=u(x,y)+iv(x,y), z=e^w=e^u+iv=e^u(cosv+isinv)=|z|(cosArgz+isinArgz), e^u=|z|,

u=ln|z|-ф-ия действ-го перемен-го

v=Argz+2pk, kÎZ

Lnz=ln|z|+i(argz+2pk)(1) Логар-ия ф-ия явл-ся многозначной, т.к. обрат-я ф-ия z=e^w явл-ся период-й с периодом 2pi. Если в фор-ле (1) зафиксировать k=k₀, то получим однозначную ф-цию, кот. наз-ся однозначной ветвью многозначной ф-ии.

26.2 Прямая в пространстве.

Дано: M₀(x_0,y_0,z₀), 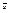(m,n,p), M₀ÎSêê 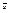. Найти ур-ие s.

MÎs Û M₀M êê 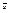Û =t ,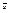

tÎ R. M₀M= , M(x,y,z)

,

параметр-ое ур-ие прямой

кононич-ое ур-ие прямой m,n,p-направляющие коэф-ты прямой, (m,n,p)¹(0,0,0)

Афинные з-чи: 1.Ур-ие пр-ой проход-ей через 2 точки.

M₀(x_0,y_0,z₀), M₁(x_1,y_1,z₁), = ,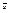

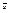=(x₁-x_0,,y₁-y_0,z₁-z₀)Þ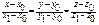

2.Условие комплонарности 2 прямых s₁ и s₂.

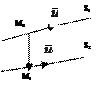Даны кононические ур-ия этих прямых. s₁ и s₂ комплонарныÛ комплонары(л/з) Û Û

Условие комплонарности 2 прямых.

Если этот определитель¹0, то s₁ и s₂ скрещиваются. Если пр-ые лежат в одной плоскости и

то s₁êês_2. Если коор-тй не пропорц-ны, то прямые пересекаются.

Прямую можно задавать как пересечение 2 плоскостей:

A₁x+B₁y+C₁z+D₁=0 (s₁) система общих ур-ий

A₂x+B₂y+C₂z+D₂=0 (s₂)

A₁m+B₁n+C₁p+=0

A₂m+B₂n+C₂p+=0 Ûm:n:p=

Метрические з-чи: угол между 2 прямыми.

Даны 2 пр. s₁ и s_2,

Найти угол(s₁,s₂).j= (s₁,s₂)= .

Þ

j=90⁰ то пр-ые перпендекулярны, соs90⁰=0.

j=0,то пр-ые парал-ны, .