Примеры выполнения заданий

Задание 1. Дана матрица А. Найти матрицу Х, удовлетворяющую условию 3 А – 2 Х = В.

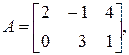
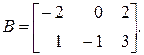
Решение

Решим уравнение 3 А – 2 Х = В в матричном виде.

Выразим из этого уравнения Х.

Так как 3 А – В = 2 Х, то Х = .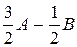

Используя линейные операции над матрицами, найдем

Х = – =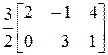

= – = ,

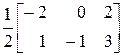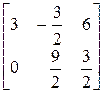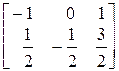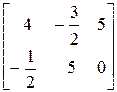откуда

Х = .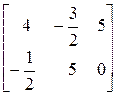

Задание 2. Найти те из произведений АВ и ВА, которые имеют смысл. Указать элемент матрицы АВ или ВА, который принадлежит строке i =2 и столбцу j =1 для

.

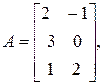
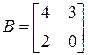Решение

Произведение матриц АВ существует, т.к. число столбцов матрицы А равно числу строк матрицы В. Найдем произведение матриц по определению:

.

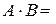
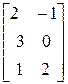
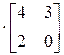
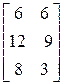Элемент .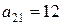

Произведение матриц ВА не существует, т.к. матрицы В и А несогласованные.

Задание 3. Вычислить ранг матрицы 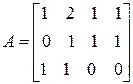с помощью элементарных преобразований.

Решение. Выполним элементарные преобразования над матрицей А.

~ ~

~ ~ ~ ,

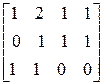
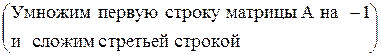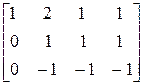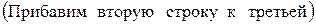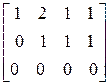Число ненулевых строк преобразованной матрицы равно 2, следовательно, ранг матрицы равен 2.

Задание 4. Решить неравенство: .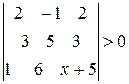

Решение

Вычислим определитель по правилу треугольников:

= =

= .

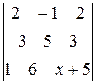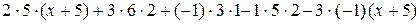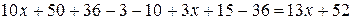Решая неравенство, 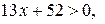найдем .

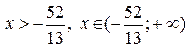Задание 5. Для данного определителя 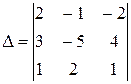и для заданных значений i = 2; j = 3, найти:

1) миноры и алгебраические дополнения элемента a _23;

2) вычислить определитель:

а) разложив его по элементам 2-й строки,

б) разложив его по элементам 3-го столбца;

3) вычислить определитель по правилу треугольников.

Решение

1)Найдем минор М ₂₃ и алгебраическое дополнение А ₂₃:

,

;

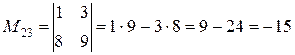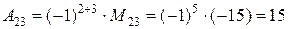2) а) вычислим определитель, разложив его по элементам второй строки:

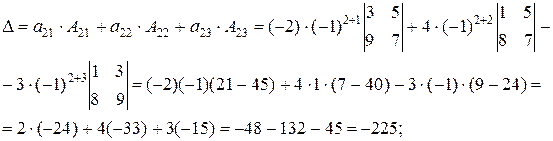
б) вычислим определитель, разложив его по элементам третьего столбца:

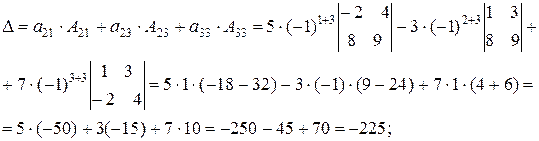
3) вычислим определитель по правилу треугольников:

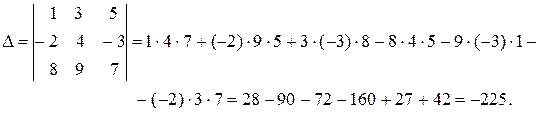
Итак, .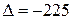

Задание 6. Найти матрицу обратную данной матрице .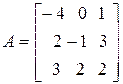

Решение

Если квадратная матрица А невырожденная, то у нее существует обратная матрица, которую найдем по формуле

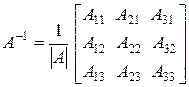, где 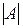– определитель матрицы А,

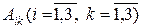, – алгебраические дополнения элементов матрицы А.

Так как

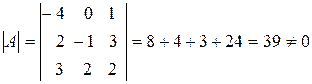, то обратная матрица существует. Составим матрицу из алгебраических дополнений элементов матрицы А. Найдем:

, , ,

, , ,

, , .

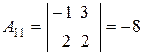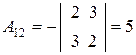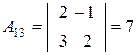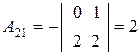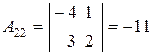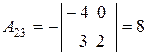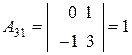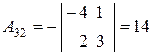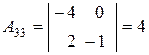Значит,

.

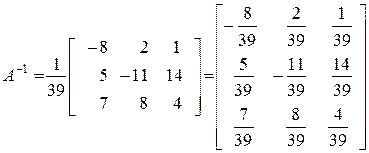Проверкой убедиться самостоятельно, что А А^-1 = А^-1 А = Е.

Задание 7. Дана система линейных неоднородных уравнений

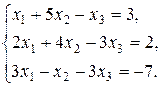
Проверить, совместна ли заданная система. В случае совместности решить её:

а) по формулам Крамера;

б) с помощью обратной матрицы (матричным методом);

в) методом Гаусса.

Решение

Формулы Крамера и матричный метод применимы, если матрица коэффициентов системы невырожденная, т.е. ее определитель отличен от нуля.

Найдем определитель

,

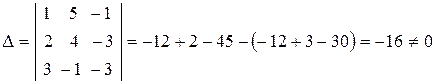а) решаем систему по формулам Крамера. Найдем 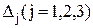– определители, полученные из определителя 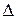заменой 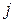-го столба столбцом их свободных членов системы, т.е.

,

,

.

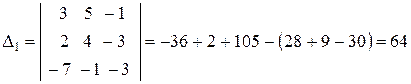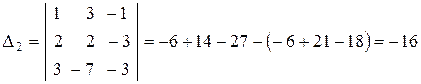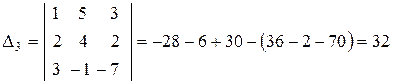Таким образом, по формулам Крамера

; ; .

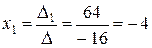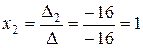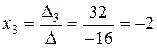Итак,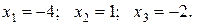

б) Из теории известно, что в матричном виде решение системы имеет вид:

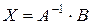, где Х = 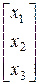, 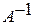– обратная матрица, В = .

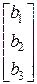Найдем 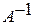(формула и процесс нахождения рассмотрены в задании 6).

, , ,

, , ,

, , ,

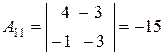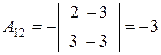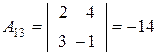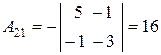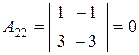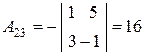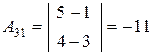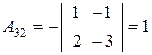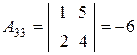Тогда

.

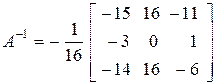Значит,

.

.

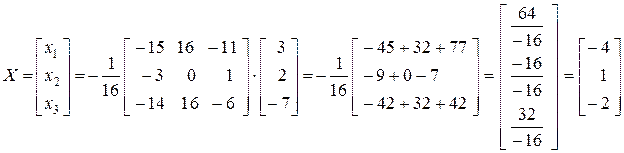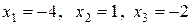Подстановкой найденных значений в уравнении системы убеждаемся в том, что они являются решением.

в) Решим систему методом Гаусса. Приведем систему к усеченному виду с помощью элементарных преобразований над ее уравнениями. Оставим первое уравнение системы без изменений и назовем его разрешающим уравнением. Исключим неизвестное 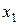из второго и третьего уравнений. Для этого обе части разрешающего уравнения умножим на 2 и вычтем полученное уравнение из второго; затем обе части разрешающего уравнения умножим на 3 и вычтем полученное уравнение из третьего. Преобразовав таким образом заданную систему уравнений, придем к эквивалентной ей системе:

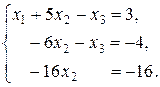
Из последнего уравнения полученной системы находим 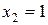. Из предпоследнего уравнения находим 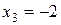, из первого уравнения находим 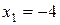. Проверкой убеждаемся, что значения 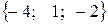, являются решением системы.

Рассмотрим общий случай системы m линейных уравнений с n неизвестными, то есть, когда число уравнений не совпадает с числом неизвестных.

Процесс решения такой системы методом Гаусса упрощается, если преобразованиям подвергнуть не систему, а её расширенную матрицу. Опишем процесс преобразований, рассмотрев один шаг гауссовых исключений.

Составим расширенную матрицу системы

.

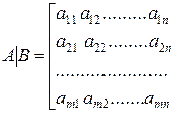
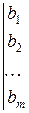
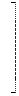В матрице 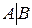выберем разрешающую строку, разрешающий столбец и разрешающий элемент, стоящий на их пересечении. Например, если 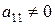, то на первом шаге гауссовых исключений первую строку и первый столбец будем считать разрешающими, 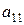– разрешающим элементом. При переходе к новой преобразованной матрице, используем следующие правила:

1) элементы разрешающей строки (и всех выше расположенных строк, если это не первый шаг) остаются неизменными;

2) элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули;

3) все прочие элементы матрицы вычисляются по правилу прямоугольника: пусть k -я строка является разрешающей, а_ks – разрешающий элемент, a_ij –пересчитываемый элемент, а_is – элемент, стоящий на пересечении разрешающего столбца и строки пересчитываемого элемента, а_kj – элемент, стоящий на пересечении разрешающей строки и столбца пересчитываемого элемента. В пересчёте всякий раз участвуют четыре элемента, составляющие определитель второго порядка.

Преобразованный элемент равен разности произведений элементов главной диагонали (главной является та диагональ, которая содержит разрешающий элемент) и побочной. То есть а_ij ′ = a_ksa_ij – a_kja_is (см. схему)

◦ ◦ ◦ ◦ ◦ ◦ ◦

◦ а_ks ◦ ◦ ◦ a_kj ◦

◦ ◦ ◦ ◦ ◦ ◦ ◦

◦ a_is ◦ ◦ ◦ a_ij ◦

◦ ◦ ◦ ◦ ◦ ◦ ◦

В частности, на первом шаге разрешающим является элемент а ₁₁. Тогда

а_ij ′ = а ₁₁ a_ij – а_{1 j} а_i1, I = 2, 3, …, m; j = 2,3, …, n.

Пересчитаем элементы всех нижележащих строк.

Осуществив последовательно необходимое число шагов гауссовых исключений (прямой ход метода Гаусса), получим матрицу эквивалентную исходной. Записываем соответствующую ей систему уравнений, из которой, начиная с последнего уравнения, последовательно находим решения системы (обратный ход метода Гаусса).

Задание 8. Решить методом Гаусса систему линейных уравнений

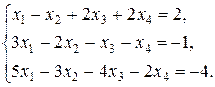
Решение

Расширенная матрица системы имеет вид

А | В = .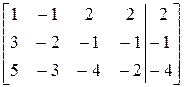

Элемент а ₁₁ = 1 ≠ 0. Первую строку и первый столбец будем считать разрешающими, элемент а ₁₁ – разрешающим. Выполним первый шаг гауссовых исключений: разрешающую строку переписываем без изменения, в разрешающем столбце ниже разрешающего элемента записываем нули, остальные элементы пересчитываем по правилу прямоугольника (все операции запишем в матрице подробно). Получим преобразованную матрицу

=

= .

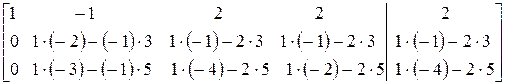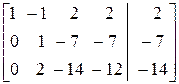На втором шаге разрешающим является элемент а ₂₂′ ≠ 0. Если он равен нулю, меняем эту строку с той нижележащей строкой, у которой коэффициент при х ₂ отличен от нуля. Первые две строки переписываем без изменения, под разрешающим элементом записываем нуль, остальные элементы пересчитываем по правилу прямоугольника. Получим преобразованную матрицу

=

= .

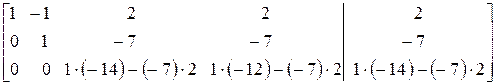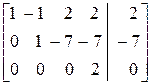Таким образом, процесс гауссовых исключений завершен. Заметим, что если система имеет т уравнений, то в общем случае необходимо осуществить т – 1 шаг гауссовых исключений. Получили матрицу эквивалентную исходной расширенной матрице. Полученная расширенная матрица имеет три ненулевых строки, значит, ее ранг равен 3. Матрица коэффициентов системы имеет также три ненулевых строки, значит, ее ранг равен 3. В системе четыре неизвестных. На основании теоремы Кронекера–Капелли заключаем, что система совместна и имеет бесчисленное множество решений. Запишем систему уравнений, соответствующую последней преобразованной матрице

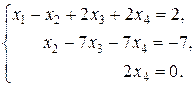
Осуществим обратный ход метода Гаусса.

Из последнего уравнения системы находим х ₄ = 0. Подставим х ₄ во второе уравнение, получим х ₂ = 7 х ₃ – 7, где х ₃ – любое действительное число. Положим х ₃ = с, тогда х ₂ = 7 с – 7. Подставим найденные х ₄, х ₃ и х ₂ в первое уравнение системы, найдём х ₁ = 5 с – 5.

Итак, получили общее решение системы: х ₁ = 5 с – 5, х ₂ = 7 с – 7 х ₃ = с, х ₄ = 0.

Выбирая в качестве с любое действительное число, можем получить бесчисленное множество частных решений.

Вопросы для самопроверки

1. Что называется матрицей? Какое различие между матрицей и опреде­лителем?

2. Какую матрицу называют транспонированной, треугольной, диагональной?

3. Сформулируйте правило сложения матриц.

4. Как составляется произведение двух матриц?

5. Какими свойствами обладает умножение матриц?

6. Какая матрица называется единичной?

7. Что называется определителем второго порядка?

8. Что называется определителем третьего порядка?

9. Сформулируйте свойства определителей третьего порядка.

10. Что называется минором определителя третьего порядка?

11. Что называется алгебраическим дополнением?

12. Какая матрица называется неособенной?

13. Какая матрица называется особенной?

14. Дайте определение определителя п -го порядка. Какие существуют правила вычисления определителей п -го порядка?

15. Какая матрица называется обратной по отношению к данной квадратной матрице?

16. Какое условие является необходимым и достаточным для существования обратной матрицы?

17. Запишите формулу для нахождения обратной матрицы.

18. Что называется рангом матрицы?

19. Какие преобразования матриц не меняют ее ранга?

20. Какая связь между рангом матрицы и числом линейно-независимых строк (столбцов)?

21. Что называется матрицей систем линейных уравнений?

22. Какой определитель называется определителем системы? Какому усло­вию должен удовлетворять определитель системы, чтобы она имела единствен­ное решение?

23. Какому условию должны удовлетворять коэффициенты системы уравнений 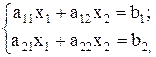чтобы система:

а) была несовместной;

б) имела единственное решение;

в) имела бесчисленное множество решений?

24. Запишите формулы Крамера для системы трех линейных уравнений с тремя неизвестными.

25. Какая система линейных уравнений называется однородной?

26. Каков порядок решения системы линейных уравнений по формулам Крамера? Когда применимо правило Крамера к решению систем?

27. Каков порядок решения системы линейных уравнений матричным методом? При каких условиях он применим?

28. Сформулируйте теорему о совместности системы линейных уравнений Кронекера-Капелли.

29. Какое условие является необходимым и достаточным для того, чтобы однородная система имела ненулевое решение?

30. Что называется одним шагом гауссовых исключений?

31. Сформулируйте правила перехода от исходной системы к новой после одного шага гауссовых исключений.

32. Каков порядок вычисления ранга матрицы с помощью гауссовых исключений?

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гантмахер, Ф.Р. Теория матриц.– М.: Наука, 1967. –576с.

2. Ланкастер, П. Теория матриц. – М.: Наука, 1978. –280с.

Date: 2015-04-23; view: 1749; Нарушение авторских прав