Свойства определителей

Перечислим свойства определителей без доказательства.

Свойство 1. Значение определителя не изменится от замены всех его строк соответствующими по номеру столбцами и обратно.

Замечание. Это свойство означает равноправие строк и столбцов определителя.

Свойство 2. Если поменять местами два столбца (строки) определителя, то определитель изменит знак на противоположный.

Свойство 3. Определитель с двумя одинаковыми столбцами (строками) равен нулю.

Свойство 4. Если все элементы какого-нибудь столбца (строки) определителя умножить на одно и то же число , то определитель умножится на число .

Следствие 1. Если все элементы какого-либо столбца (строки) определителя имеют общий множитель, то его можно вынести за знак определителя.

Следствие 2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то и сам определитель равен нулю.

Свойство 5. Определитель, у которого элементы двух столбцов (строк) соответственно пропорциональны, равен нулю.

Определение 1.8. Минором определителя 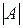(или квадратной матрицы А), соответствующим элементу , будем называть определитель, полученный из данного, если в нём вычеркнуть 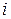-ю строку и 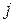-й столбец, на пересечении которых стоит элемент . Обозначают минор символом .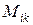

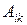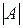Определение 1.9. Алгебраическим дополнением элемента определителя (или квадратной матрицы А) называют соответствующий этому элементу минор, взятый со знаком 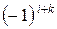, т.е. = .

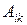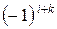
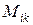Пример

Дан определитель = .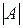

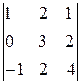Тогда = ; .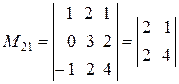

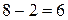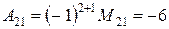Свойство 6. Определитель равен сумме произведений элементов какого-либо столбца (строки) на их алгебраические дополнения:

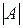= (1.4)

.

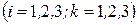Запись определителя, согласно какой-либо из формул (1.4), при определённых значениях 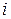и 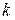называется разложением определителя по элементам 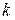-го столбца (или 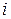-й строки). Формулы (1.4) являются правилом вычисления определителей.

Пример. Вычислить определитель

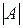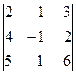= , разлагая его по элементам 2-й строки.

Date: 2015-04-23; view: 729; Нарушение авторских прав