Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение. Замечание.Свойство 6 позволяет ввести понятие определителя -го порядка
|
|
= 
= 
.
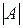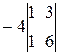
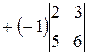
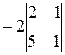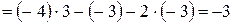Замечание. Свойство 6 позволяет ввести понятие определителя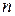 
-го порядка.
Под определителем 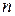-го порядка понимают число
= 
= 
, 
.
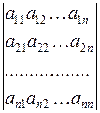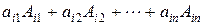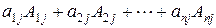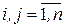Свойство 7. Сумма произведений элементов какого-либо столбца (строки) определителя на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.
Свойство 8. Если каждый элемент какого-либо столбца (строки) определителя 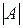есть сумма двух слагаемых, то определитель равен сумме двух определителей, причём в одном из них соответствующий столбец (строка) состоит из первых слагаемых, а в другом – из вторых слагаемых.
Свойство 9. Определитель не меняет своего знака от прибавления ко всем элементам какого-либо столбца (строки) определителя соответствующих элементов другого столбца (строки), умноженных на одно и то же число.
ТЕМА: Ранг матрицы и его вычисление. Обратная матрица, её определение, вычисление, основные свойства. Системы линейных уравнений. Матричная запись. Теорема Кронекера-Капелли (формулировка). Методы решения систем линейных уравнений.
Date: 2015-04-23; view: 453; Нарушение авторских прав