Ранг матрицы

Рассмотрим прямоугольную матрицу , .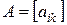

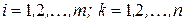Определение 2.1. Определитель порядка 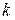, составленный из элементов, стоящих на пересечении выделенных 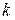строк и 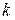столбцов матрицы , называется минором 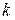– го порядка данной матрицы 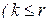, где .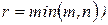

Определение 2.2. Рангом матрицы называется наибольший из порядков отличных от нуля миноров, порождаемых данной матрицей.

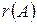Из определения следует, что рангом обладает каждая матрица. Если все элементы матрицы равны нулю, то ранг её равен 0, а сама матрица называется нуль-матрицей. Ранг матрицы обозначают через . Если все миноры некоторого порядка 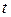данной матрицы равны нулю, то ранг её меньше 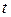. Так как количество миноров различного порядка матрицы велико, то вычисление ранга, основанного на последовательном вычислении её миноров от самого высшего порядка и ниже, весьма затруднительно. Существуют приёмы более простые в применении. Например, основанный на следующей теореме.

Теорема 2.1. (без доказательства).

Ранг матрицы не меняется, если:

все строки матрицы заменить соответствующими столбцами, т. е. матрицу протранспонировать;

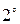поменять местами две строки (столбца);

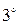умножить каждый элемент любой её строки (столбца) на один и тот же множитель, отличный от нуля;

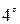сложить любую её строку (столбец) с другой строкой (столбцом), умноженной на .

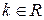Перечисленные в теореме 2.1. преобразования называются элементарными.

Замечание. Матрицу, полученную из заданной путём элементарных преобразований, называют эквивалентной матрицей.

Конкретные примеры вычисления ранга матрицы на основании этой теоремы будут рассмотрены в разделе практических приложений.

В разделе «Векторная алгебра» изучено понятие линейной зависимости и линейной независимости векторов, которое может быть перенесено на строки (столбцы) матрицы, если их элементы отождествлять с координатами векторов. В связи с этим полезно рассмотреть связь между рангом матрицы и числом линейно независимых строк или столбцов.

Теорема 2.2. (без доказательства).

Если ранг матрицы равен 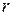, то у нее существует 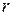линейно независимых строк (столбцов), через которые линейно выражаются все остальные строки (столбцы).

Следствие 1. Максимальное число линейно независимых строк (столбцов) матрицы равно её рангу.

Замечание. Если – квадратная матрица и её определитель равен нулю, то одна из строк (столбцов) есть линейная комбинация остальных строк (столбцов).

Date: 2015-04-23; view: 517; Нарушение авторских прав