Определители 2-го и 3-го порядков и их свойства

Определение 1.6. Определителем второго порядка называется число .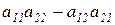

Обозначается определитель символом

.

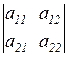Таким образом,

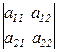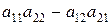= . (1.2)

Об определителе (1.2) говорят, что он соответствует квадратной матрице 2-го порядка

.

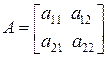Числа 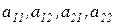– элементы определителя. Элементы 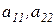образуют главную диагональ, элементы 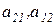– побочную диагональ определителя. Если речь идёт об определителе квадратной матрицы , то имеют место обозначения: , , .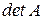

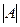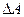Пример

Вычислить определитель матрицы .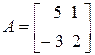

= = = .

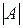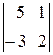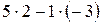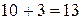Определение 1.7. Определителем третьего порядка называют число, которое обозначается и равно

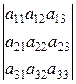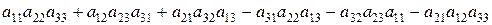= . (1.3)

Для запоминания формулы (1.3) удобно пользоваться правилом треугольников (правилом Саррюса), согласно которому первые три слагаемые правой части равенства (1.3) вычисляются, как это показано на рис. 1.1; они представляют собой произведение элементов, стоящих на главной диагонали и в вершинах треугольников, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемые вычисляются аналогично (рис. 1.2.), только за основу берётся побочная диагональ и берутся они с обратным знаком:

+ –

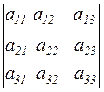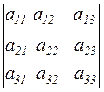
Рис 1.1. Рис 1.2.

Квадратную матрицу будем называть особой (или вырожденной), если 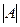=0. В противном случае квадратная матрица называется неособой (или невырожденной).

Date: 2015-04-23; view: 601; Нарушение авторских прав