Действия над матрицами

Определение 1.2. Суммой двух матриц и 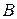одинаковой размерности 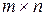называется матрица 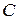такой же размерности, элементы которой равны сумме соответствующих элементов матриц и 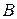: 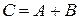, если .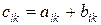

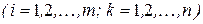Операция нахождения суммы данных матриц называется сложением матриц.

Пример

+ = = .

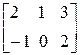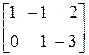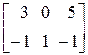Из определения сложения матриц следует, что эта операция обладает свойствами:

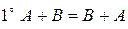(переместительное);

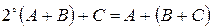(сочетательное).

Операция сложения матриц естественным образом распространяется на случай любого конечного числа слагаемых.

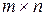Определение 1.3. Произведением матрицы размерности на число из 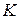называется матрица 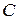размерности 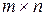, элементы которой получаются из соответствующих элементов матрицы умножением на число :

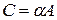, если .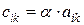

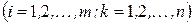Операция называется умножением матрицы на число.

Пример

= .

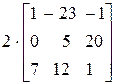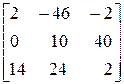Свойства операции умножения матрицы на число.

,

,

.

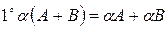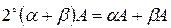Следствие. Разность 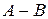двух матриц одинаковой размерности 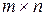определяется равенством .

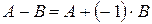Определение 1.4. Произведением двух матриц и 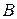называется матрица 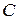, у которой элемент 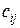, стоящий на пересечении 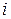- й строки и 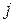- го столбца, равен сумме попарных произведений элементов 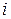- й строки матрицы на элементы 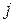-го столбца матрицы :

= = .

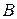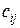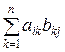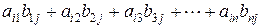
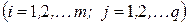Замечание. Операция умножения двух прямоугольных матриц выполнима лишь в том случае, когда число столбцов в первом сомножителе равно числу строк во втором. Такие матрицы называют согласованными (или соответственными).

В частности, умножение всегда выполнимо, если матрицы и 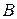квадратные одного и того же порядка.

Пример

= =

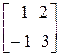
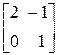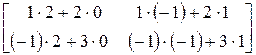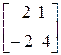
Если 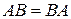, то матрицы называют перестановочными или коммутирующими между собой.

Пример

Матрицы

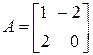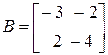, перестановочны между собой, так как

, .

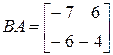Свойства операции умножения матриц.

;

;

.

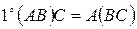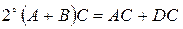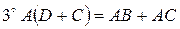Операция умножения матриц естественным образом распространяется на случай нескольких сомножителей.

Определение 1.5. Матрицу В размерности 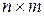называют транспонированной матрице размерности 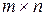, если строки и столбцы матрицы с сохранением порядка их следования поменять местами, то есть первая строка матрицы меняется на первый столбец, вторая строка – на второй столбец и т.д. Обозначают транспонированную матрицу .

Пример

, .

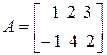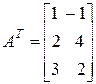Две матрицы и 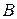называют равными, если они одинаковой размерности и соответствующие элементы равны между собой.

Date: 2015-04-23; view: 441; Нарушение авторских прав