Обратная матрица, её определение, вычисление, основные свойства

Определение 2.3. Матрица называется обратной к квадратной матрице , если , где 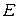– единичная матрица.

Теорема 2.3. (без доказательства).

Для существования обратной матрицы необходимо и достаточно, чтобы 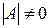, т.е. чтобы матрица была невырожденной (неособенной).

Прежде чем записать формулу для вычисления обратной матрицы, введём следующее понятие.

Матрицу

,

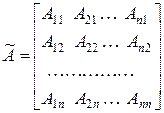составленную из алгебраических дополнений к элементам матрицы , называют присоединённой к матрице .

Формула для вычисления матрицы, обратной для невырожденной матрицы , имеет вид:

(2.1).

Системы линейных уравнений. Матричная запись. Теорема Кронекера-Капелли (формулировкa)

Рассмотрим систему m линейных уравнений с n неизвестными :

(2.2)

Введём обозначения матриц:

– матрица коэффициентов системы;

– матрица неизвестных;

– матрица правых частей (или свободных членов);

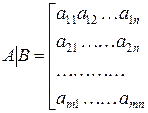
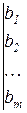
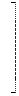– расширенная матрица системы.

Тогда на основании правила умножения матриц заменим систему (2.2) матричным уравнением с неизвестной матрицей :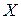

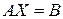. (2.3)

В частности, если 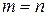, матрица является квадратной. В этом случае имеем систему 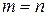уравнений с 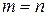числом неизвестных.

Систему уравнений (2.2) будем называть совместной, если можно найти такие значения неизвестных , которые удовлетворяют всем уравнениям системы (т.е. при подстановке обращают все уравнения в верные равенства). Совокупность этих значений будем называть решением системы.

Заметим, что таких значений может не быть, тогда система называется несовместной.

Теорема 2.4. (Кронекера - Капелли)

Для того чтобы система линейных уравнений (2.2) была совместной, необходимо и достаточно, чтобы ранг её матрицы равнялся рангу расширенной матрицы 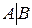. Если ранг матрицы равен рангу расширенной матрицы 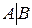и равен числу неизвестных n, то система имеет единственное решение. Если ранг матрицы равен рангу расширенной матрицы 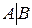, но меньше числа неизвестных, то система имеет бесчисленное множество решений.

Замечание 1. Ранг матрицы больше числа неизвестных быть не может.

Замечание 2. Если , то система (2.2) называется однородной.

Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ранг ее матрицы коэффициентов меньше числа неизвестных. Из теоремы 2.4 следует, что такая система всегда совместна, так как она всегда имеет решение 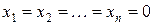, которое называется тривиальным или нулевым.

В частности, если однородная система n линейных уравнений с n неизвестными, то она обладает ненулевым решением, если её матрица коэффициентов вырожденная.

Date: 2015-04-23; view: 488; Нарушение авторских прав