Правило Крамера

Рассмотрим систему n линейных уравнений с n неизвестными (система (2.2) при 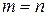). Тогда матрица коэффициентов этой системы будет квадратной. Её определитель 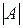обозначим символом .

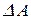Теорема 3.1. Если определитель 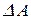системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, которое может быть получено по формулам:

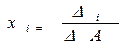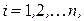, (3.1)

где 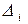- определители, полученные из 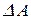заменой в нём 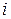-го столбца столбцом из свободных членов.

Доказательство

Так как определитель системы 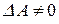, то решение можно записать в матричной форме (2.4):

.

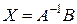Перейдём к развёрнутой форме записи решения:

.

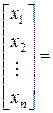
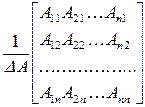
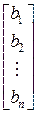Выполнив операцию умножения матриц в правой части, получим

,

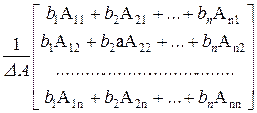откуда

,

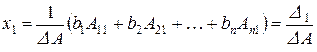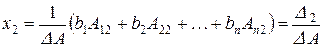, (3.2)

.

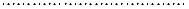
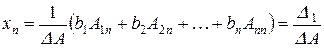Таким образом, теорема доказана.

Формулы (3.2) для нахождения решения системы называется формулами Крамера.

Примеры будут рассмотрены в разделе практических приложений.

Метод Гаусса (последовательного исключения неизвестных)

Практическое значение рассмотренных выше методов решения линейных систем (матричный метод и правило Крамера) невелико, так как их применение ограничено. Они применимы только в том случае, когда матрица коэффициентов системы квадратная и невырожденная. Кроме того, оба метода достаточно «трудоёмки». Более удобным является метод Гаусса – последовательного исключения неизвестных.

Рассмотрим систему линейных уравнений (2.2) для случая 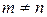(т.е. общий случай).

Назовём элементарными преобразованиями системы линейных уравнений следующие операции.

1. Умножение какого-либо уравнения на число, не равное нулю.

2. Прибавление к любому уравнению другого уравнения, умноженного на произвольное число.

3. Перемена местами уравнений в системе.

С помощью таких преобразований полученная система уравнений равносильна исходной.

Суть метода Гаусса состоит в том, что путём элементарных преобразований над уравнениями системы она приводится к «усечённому»

виду (матрица коэффициентов трапециевидная), после чего её решение найти несложно.

Покажем, как эти преобразования осуществить, проделав только один шаг гауссового исключения (в силу громоздкого описательного характера).

Пусть в системе

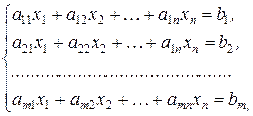(3.3)

коэффициент .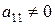

Если он равен нулю, на первое место ставим уравнение, в котором коэффициент при неизвестном 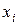будет отличен от нуля. Умножая обе части первого уравнения данной системы поочерёдно на 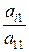и вычитая всякий раз из 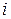- го уравнения 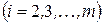, придём к системе, у которой во всех уравнениях, начиная со второго, отсутствует неизвестное :

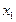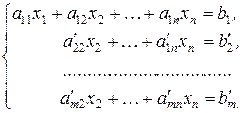(3.4)

В системе (3.4) через 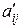обозначены новые коэффициенты. Коэффициент 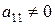на первом шаге называют разрешающим, первое уравнение – разрешающим уравнением, столбец коэффициентов при 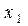– разрешающим столбцом.

Далее поступаем аналогично. Предположив, что 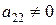, переходим на втором шаге к равносильной системе, в которой во всех уравнениях, начиная с 3-го, отсуствует неизвестное .

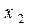Правило преобразования коэффициентов и свободных членов системы (3.3) при переходе на каждом шаге к равносильной системе «усечённого» вида можно сформулировать так:

1) коэффициенты и свободный член разрешающего уравнения остаются без изменения;

2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;

3) все прочие коэффициенты и свободные члены пересчитываются.

Для пересчёта коэффициентов можно пользоваться так называемым правилом прямоугольника. Это правило будет показано на конкретном примере в разделе практических приложений. Процесс преобразования исходной системы к «усечённой» называется прямым ходом метода Гаусса. При осуществлении прямого хода метода Гаусса может сложиться ситуация, когда преобразованное уравнение будет иметь вид:

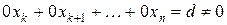и тогда данная система несовместна. Если же встретится уравнение вида: 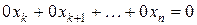, то такое уравнение следует отбросить и далее не рассматривать.

Осуществив до конца прямой ход метода Гаусса, получим систему:

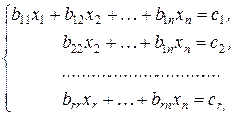(3.5)

где 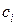, 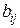– новые преобразованные коэффициенты, причем 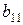, , 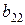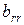отличны от нуля. Такую запись системы называют ступенчатой. В частности, при 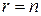она будет иметь треугольный вид.

Если 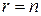, то последнее уравнение системы (3.5) будет иметь вид: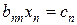 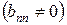, откуда 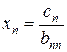. Затем из предпоследнего уравнения находим 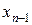, затем из третьего от конца 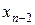и т. д. Двигаясь таким образом снизу вверх, найдём все неизвестные. Эту процедуру называют обратным ходом метода Гаусса.

Если 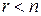, то из последнего уравнения выражаем 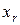через 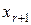, , 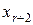, 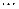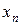. И затем аналогично двигаемся снизу вверх, отыскивая 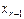, , , 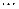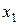. Таким образом, неизвестные 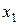, , 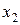, 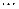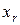(их называют базисными) выражаются через 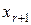, , 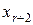, 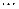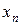(их называют свободными).

Построенное решение называют общим решением системы (3.5).

Поскольку свободные неизвестные могут принимать любые числовые значения, каждый раз будет получаться определённое частное решение исходной системы. В рассмотренном случае система имеет бесчисленное множество решений. Заметим, что частное решение, полученное из общего при нулевых значениях свободных неизвестных, называется базисным решением.

Процесс решения системы линейных уравнений методом Гаусса можно значительно облегчить, если преобразования проводить над строками расширенной матрицы этой системы. Преобразования 2), 3), 4), указанные в теореме 2.1, применительно к матрицам, также являются элементарными и не меняют её ранга.

Расширенная матрица преобразованной системы

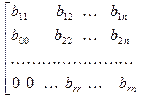
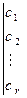
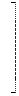
эквивалентна расширенной матрице 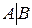исходной системы. Значит, ранги их равны. Ранг преобразованной матрицы будет равен числу её ненулевых строк.

Результат проведенных выше рассуждений (что полностью согласуется с теоремой Кронекера – Капелли) следующий: если r = n, т.е. ранг системы уравнений равен числу неизвестных, то система имеет единственное решение; если r 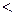n, то система имеет бесчисленное множество решений; r 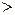n быть не может.

Примеры будут рассмотрены в разделе практических приложений.

Date: 2015-04-23; view: 655; Нарушение авторских прав