Понятие матрицы. Основные обозначения

Министерство образования Республики Беларусь

Учреждение образования

МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРОДОВОЛЬСТВИЯ»

Кафедра «Высшая математика»

С.В. Подолян, Т.М. Гончарова, И.В.Юрченко

ВЫСШАЯ МАТЕМАТИКА

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Учебно-методическое пособие

для студентов специальности

1-53 01 01 «Автоматизация технологических процессов и производств»

Могилев 2008

УДК 519.21 517

Рассмотрено и рекомендовано к изданию

На заседании кафедры высшей математики

Протокол № 5 от 26.12. 2007 г.

УМС по специальности 1-53 01 01

«Автоматизация технологических процессов и производств»

Протокол № 2 от 18.01. 2008г.

Научно-методическим Советом университета

Протокол № 4 от 05.02. 2008г.

Составители:

С.В.Подолян, Т.М. Гончарова, И.В. Юрченко

Рецензенты:

кандидат физико-математических наук, доцент кафедры ВМ УО МГУП

Лапковский В.К.

кандидат физико-математических наук, доцент кафедры ВМ УО БРУ

Данилович Л.А.

Учебно-методическое пособие предназначено для самостоятельного изучения студентами основ линейной алгебры: матрицы, действия с ними; определители, их свойства и вычисление; решение систем линейных алгебраических уравнений и соответствует рабочей программе.

Теоретическая часть сопровождается примерами решения задач, вопросами для самоконтроля. Указан список литературы, которой студент может воспользоваться дополнительно в случае необходимости.

© Учреждение образования

«Могилевский государственный

университет продовольствия», 2008

ТЕОРИТИЧЕСКАЯ ЧАСТЬ

ТЕМА: Понятие матрицы. Основные обозначения. Виды матриц. Действия над матрицами: сложение и умножение. Определители 2-го и 3-го порядков и их свойства. Понятие определителя n-го порядка.

Понятие матрицы. Основные обозначения

Пусть дана некоторая совокупность чисел К, в пределах которой всегда выполнимы и однозначны четыре операции: сложение, вычитание, умножение и деление на число, отличенное от нуля. Примерами таких совокупностей чисел могут служить совокупность (или множество) всех рациональных чисел, совокупность всех действительных чисел.

Определение 1.1. Прямоугольную таблицу чисел из совокупности К

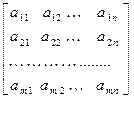(1.1)

будем называть матрицей.

Если 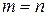, то матрица называется квадратной, а число 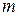, равное 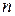, называется её порядком. В общем же случае, когда 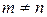, матрица называется прямоугольной размера 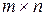или 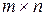– матрицей. Числа, составляющие матрицу, называются её элементами.

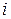При двухиндексном обозначении элементов матрицы , первый индекс указывает номер строки, а второй индекс k – номер столбца, на пересечении которых стоит данный элемент.

Наряду с обозначением матрицы (1.1) в квадратных (или круглых) скобках, будем использовать сокращённое обозначение

.

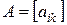
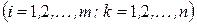Матрицу будем обозначать также одной заглавной буквой, например, матрица , матрица 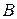и т. д.

Date: 2015-04-23; view: 433; Нарушение авторских прав