Деякі застосування визначників. Обчислення рангу матриці

Теорема 1. Для того, щоб детермінант квадратної матриці дорівнював нулю, необхідно і достатньо, щоб ранг цієї матриці був менший її порядку.

Наслідок 1. Детермінант дорівнює нулю тоді і тільки тоді, коли його рядки (стовпці) утворюють лінійно залежну систему векторів.

Наслідок 2. Квадратна матриця є особливою тоді і тільки тоді, коли її детермінант дорівнює нулю.

Наслідок 3. Добуток двох неособливих матриць – неособлива матриця. Добуток двох матриць, хоча б одна з яких особлива, - особлива матриця.

Нехай дана прямокутна матриця А =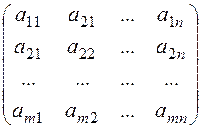

Теорема. (про ранг матриці) Для того, щоб ранг матриці дорівнював r, необхідно і достатньо, щоб серед мінорів матриці знайшовся хоча б один мінор r-го порядку, відмінний від нуля, а всі його мінори (r+1)-го порядку дорівнювали нулю.

Означення. Рангом матриці називається найвищий порядок мінорів цієї матриці, відмінних від нуля.

Приклад. Обчислити ранг матриці методом окантування мінорів:

А =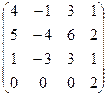

М₁ ¹ 0

M₂ = 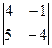= -16+5 = -11

M₃ = = -48-6-45+12+72+15 = 0

M₃ = 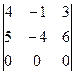= 0

M₃ = 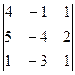= -16-2-15+4+5+24 = 0

M₃ = = 2(-1)⁶ 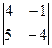= -22 ¹ 0

M₄ = 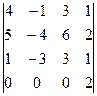= 2 = 0 r(A) = 3

Перевірка:

r(A) = 3

Date: 2015-04-23; view: 559; Нарушение авторских прав