Матриці

Означення. Матрицею називається прямокутна таблиця, яка складається з елементів даного поля.

Загальний вигляд матриці:

A = = (а_ij), А = (a₁,a₂,…,a_n), В =

де а_ij,а_i,b_j - елементи матриці.

Якщо в матриці А кількість рядків дорівнює кількості стовпців, тобто m=n, то вона називається квадратною матрицею n-го порядку; якщо ж m¹n, то матриця називається прямокутною матрицею розміру m*n. Головною діагоналлю квадратної матриці n-го порядку називається діагональ, яка йде від лівого верхнього кута до нижнього правого, тобто яка складається з елементів а₁₁,а₂₂,…,а_nn.

Означення. Квадратна матриця D=(d_ij) n-го порядку називається діагональною, якщо всі її елементи, які не належать головній діагоналі, дорівнюють нулю:

"i, j (i¹ j => d_ij=0).

Елемент головної дігоналі матриці називають i-им дігональним елементом.

Діагональна матриця називається скалярною, якщо елементи її головної діагоналі рівні між собою. Діагональна матриця: D =

Скалярна матриця: K =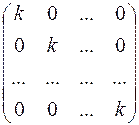

Частинним випадком скалярної матриці є одинична E і нульова O:

E = 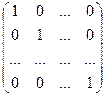q =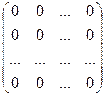

Дві матриці називаються рівними, якщо рівні відповідні їх елементи.

Від матриці А можна перейти до матриці А¢:

A¢ =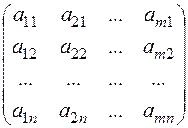

в якій рядки є стовпцями, а стовпці – рядками матриці А. Перехід від матриці А до матриці A¢ називається транспонуванням матриці А, а матриця А¢ називається транспонованою для матриці А. Якщо матриця
А – квадратна, то її транспонування – це заміна кожного рядка матриці на відповідний стовпчик.

Якщо А – довільна квадратна матриця і A¢=A,

то А називається симетричною; якщо A¢=-А,

то А - кососиметрична.

Квадратна матриця ортогональна, якщо АА¢=A¢A=E.

Матриця називається ідемпотентною, якщо А²=А.

Date: 2015-04-23; view: 631; Нарушение авторских прав