Обернена матриця

Означення. Матрицею, оберненою до матриці А, називається матриця А^-1, яка має таку властивість

АА^-1=А^-1А=Е, де Е – одинична матриця відповідного порядку.

Матриця, для якої існує обернена їй матриця, називається оборотною.

Наслідки. 1. Е^-1=Е;

2. (А^-1)^-1=А;

3. Лише квадратна матриця має обернену, причому її порядок такий же, як і порядок даної матриці.

Означення. Квадратна матриця називається особливою (виродженою), якщо її ранг менший її порядку. Квадратна матриця, яка не є особливою, є неособливою (невиродженою).

Теорема 1. Довільна неособлива матриця елементарними перетвореннями рядків може бути зведена до одиничної матриці.

Теорема 2. Матриця має обернену тоді і тільки тоді, коли вона неособлива.

Алгоритм відшукання оберненої матриці:

1) Переконатися, що матриця невироджена;

2) Записати дану матрицю А і дописати справа від неї одиничну матрицю такої ж розмірності;

3) Застосовуючи елементарні перетворення до ‘подвійної матриці’, зводимо матрицю А до одиничної, тоді та матриця, яка з’являється на місці одиничної і є оберненою до матриці А.

Приклад.

1)Знайти обернену матрицю до матриці А

А =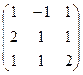

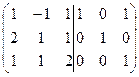
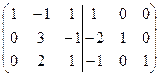
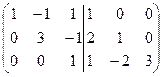
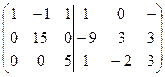
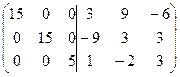
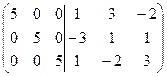
А^-1 =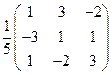

Перевірка: =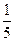

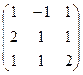
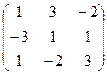Date: 2015-04-23; view: 610; Нарушение авторских прав