Ранг матриці

Розглянемо матрицю А =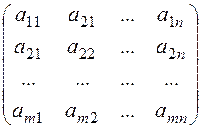

Кожний рядок матриці – це n-мірний числовий вектор, кожний стовпчик - m-мірний числовий вектор.

Означення. Ранг системи векторів-стовпчиків матриці А називається стовпчиковим рангом матриці; ранг системи векторів-рядків матриці А називається рядковим рангом матриці А.

Означення. Елементарними перетвореннями матриці є:

1) перестановка рядків (стовпчиків);

2) множення рядка (стовпчика) на довільне, відмінне від нуля число;

3) додавання рядків (стовпчиків);

4) множення рядка (стовпчика) і додавання його до іншого рядка (стовпчика).

Рангом матриці називається кількість лінійно незалежних векторів-рядків цієї матриці.

Обчислюють ранг матриці за допомогою елементарних перетворень, зводячи матрицю до виду трикутника або трапеції. Ранг матриці дорівнює кількості ненульових рядків в остаточній матриці. Якщо методом елементарних перетворень матриця звелася до виду трикутника, то її ранг дорівнює кількості векторів-рядків в даній матриці, а сама система векторів-рядків є лінійно незалежною. Якщо остання матриця набуває виду трапеції (тобто з’являються нульові рядки в ході елементарних перетворень), то ранг матриці менший, ніж кількість рядків в ній і дорівнює кількості ненульових рядків, а сама система векторів є лінійно залежною.

Розвязуючи задачу про знаходження рангу матриці, ми одержуємо не лише ранг матриці,а й ранг системи векторів-рядків,а також базис цієї системи векторів-рядків. Базис системи векторів-рядків утворюють лінійно незалежні вектори-рядки, які при елементарних перетвореннях не обнулилися.

Приклад.

1) Обчислити ранг матриці в залежності від параметра k:

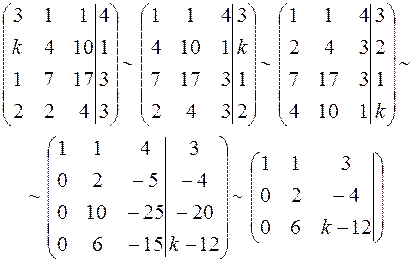
1. Якщо k-12=12 => k=0, то r=2;

2. Якщо k¹0, то r=3.

Date: 2015-04-23; view: 1042; Нарушение авторских прав