Матрична форма системи лінійних рівнянь

Нехай дана система лінійних рівнянь

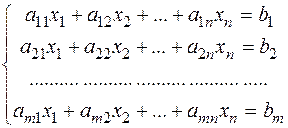
Дану систему можна записати у матричній формі

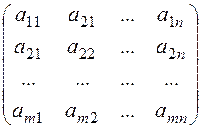
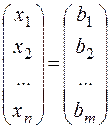
або скорочено АХ=В,

де А – матриця системи розміру m*n, а X і B – n- i m-мірні вектори-стовпці:

X = 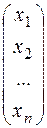B =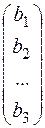

які називаються вектором невідомих і вектором вільних членів відповідно.

Якщо В=О, то одержимо матричну форму СЛОР: АХ=О.

Щоб розвязати СЛР так званим “матричним методом”, необхідно розвязати матричні рівняння виду:

а) АХ=В, тоді домножимо обидві частини рівняння на А^-1 зліва

А^-1AX=A^-1B => EX=A^-1B =>X=A^-1B.

б) ХА=В, тоді домножимо обидві частини рівняння на А^-1 справа

XAA^-1=BA^-1 => XE=BA^-1 => X=BA^-1.

в) АХВ=С, тоді домножимо обидві частини рівняння на A^-1 зліва і на В^-1 справа.

А^-1AXBB^-1=А^-1CB^-1 => EXE=А^-1CB^-1 => X=А^-1CB^-1

Приклади.

1) Розв’язати рівняння:

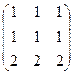
Х =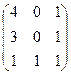

ХА=В => XAA^-1=BA^-1 => X=BA^-1

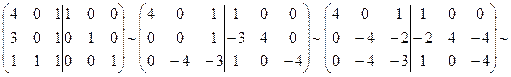
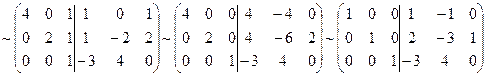
A =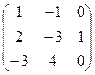

Перевірка: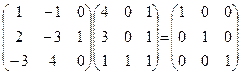

X =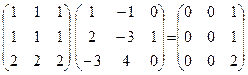

2) Розв’язати рівняння:

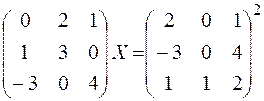
AX=B => A^-1AX=A^-1B² => X=A^-1B²

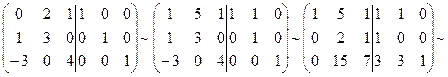
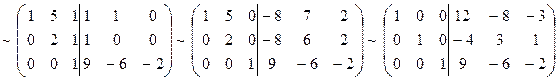
A^-1 =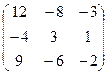

Перевірка: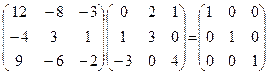

X =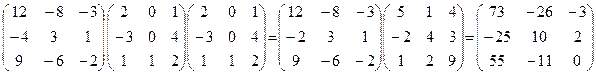

3) Розв’язати рівняння:

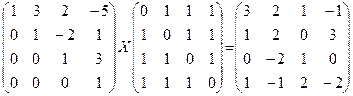
AXB=C => XB=A^{-1C => X=A-1}CB^-1

1.

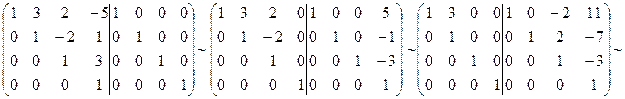
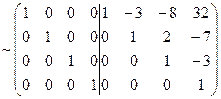A^-1 =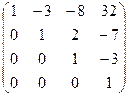

2. A^{-1C =}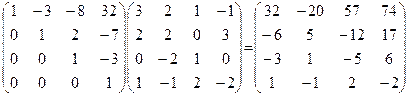

3.

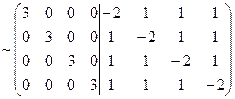
B= -⅓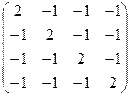

X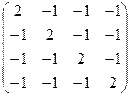= -⅓ = -⅓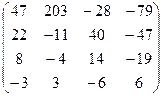

5) Обчислити f(A), якщо

(x+E₃)f(A)=x²-x+2, A=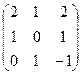

1. A+E₃ = 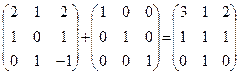= B

Bf(A) = C => f(A) = B^-1C

C = AA-A+2E =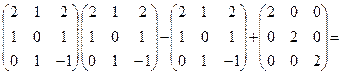

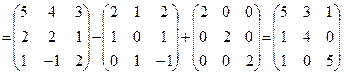
2. Знайдемо B^-1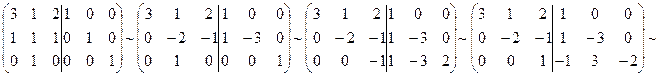

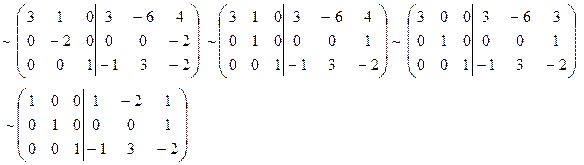
B^-1 =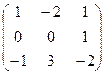

Перевірка: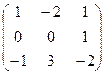

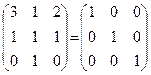
f(A) = B^{-1C =}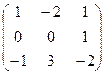

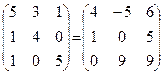
Date: 2015-04-23; view: 632; Нарушение авторских прав