Дії з матрицями

Означення. Нехай дано матриці А=(а_ij)_m*n, В=(b_ij)_m*n над полем Р. Матриця (а_ij+b_ij)_m*n називається сумою матриць А і В і позначається А+В; при цьому матриці А,В називаються доданками. Операція, яка матрицям А і В ставить у відповідність матрицю А+В називається сумою матриць. А+В=(а_ij+b_ij)

Властивості додавання матриць:

1) Операція додавання матриць комутативна, тобто для А=(а_ij)_m*n, В=(b_ij)_m*n однакового розміру А+В=В+А;

2) Операція додавання матриць асоціативна, тобто А=(а_ij)_m*n, В=(b_ij)_m*n, С=(с_ij)_m*n однакового розміру (А+В)+С=А+(В+С);

3) В множині матриць А даного розміру існує одна матриця О, яка є нейтральним елементом відносно операції додавання матриць, тобто така, що "А A+О=О+A=A, її називають нульовою матрицею;

4) В множині матриць даного розміру для кожної матриці А існує єдина протилежна матриця А¢¢, тобто така, що A+A¢¢=A+A¢¢=O.

Приклад. Дано матриці А і В. Знайти А+В і В+А і порівняти їх.

A = 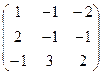B =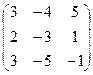

A+B =

B+A =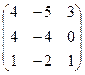

Отже, А+В=В+А.

Приклад. Дано матриці А і В. Знайти А+В.

А = B =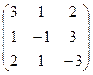

Сума матриць А+В, В+А не існує, оскільки матриці різної розмірності.

Умови існування суми матриць: матриці повинні бути однакового розміру.

Означення. Нехай дана матриця А=(а_ij)_m*n над полем Р і елемент k є Р. Добутком матриці А на елемент k називається матриця (kа_ij)_m*n, яка позначається kA.

Властивості множення матриці на скаляр:

1) Операція множення матриці на скаляр асоціативна в тому розумінні, що для довільної матриці А і чисел k,l є Р:

k(lA)=(kl)A=klA;

2)Операція множення матриці на скаляр дистрибутивна відносно додавання матриць і відносно додавання скалярів, тобто

"A "k,l є Р (k+l)A=kA+lA

"A,B "k є Р k(A+B)=kA+kB,

де А і В однакового розміру.

Приклад. Дано матриці А і В, скаляри k,l. Знайти (k+l)A,k(A+B).

A = 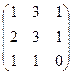B = 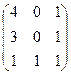k=2, m=-1

(k+m)A = (2-1)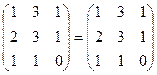

k(A+B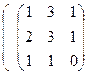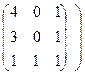) = 2 + = 2

Означення. Дано матриці А=(а_ij)_m*n і В=(b_sk)_n*l, які належать полю Р. Матриця (с_pq)_m*l, де с_pq=a_p1b_1q+a_p2b_2q+…+a_pnb_nq

називається добутком матриці А на матрицю В і позначається АВ. При цьому матриця А називається лівим множником, матриця В – правим множником. Операція, яка матрицям А і В ставить у відповідність матрицю АВ, називається множенням матриць.

Отже, АВ=(с_pq), де с_pq=a_p1b_1q+a_p2b_2q+…+a_pnb_nq,

тобто с_pq є сумою добутків відповідних елементів р-го рядка і q-го стовпчика.

Зауваження. Добуток мартиць існує тоді і лише тоді, коли кількість стовпчиків першої матриці дорівнює кількості рядків другої матриці.

Властивості множення матриць:

1) Операція множення матриць в загальному випадку некомутативна. Але існують такі матриці А,В, що АВ=ВА.

Наприклад, АЕ=ЕА=А, АО=ОА=О. Якщо матриці А і В задовольняють умову АВ=ВА, то такі матриці є перестановочними або комутативними. Комутативними є лише квадратні матриці.

2) Операція множення асоціативна, тобто

"А,В,С (АВ)С=А(ВС)

3) Асоціативність множення матриці на матрицю і на скаляр

"А,В "k,l є Р (kA)B=k(AB)

A(kB)=(Ak)B=(kA)B

4) В множині квадратних матриці n-го порядку існує єдина матриця E, яка є нейтральним елементом відносно операції множення матриць, тобто така, що "А (AE=EA=A)

Для множини прямокутних матриць А розміром m*n можна говорити про існування односторонніх нейтральних елементів, тобто таких матриць В і С, що "А (АВ=СА=А).

Операції додавання і множення матриць А і В одночасно можна виконувати лише тоді, коли А і В – квадратні матриці одного порядку.

В множині квадратних матриць n-го порядку мають місце дистрибутивні закони (правий і лівий) множення відносно додавання:

"А,В,С- n-го порядку (А+В)С=АС+ВС

С(А+В)=СА+СВ.

З сказаного вище слідує, що множина всіх квадратних матриць n-го порядку над полем Р є кільцем з одиницею відносно операцій додавання і множення матриць (некомутативне кільце). Позначається М_n=<Mat 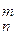(R),+,*>.

Date: 2015-04-23; view: 705; Нарушение авторских прав