Детермінант n-го порядку

Означення. Детермінантом n-го порядку квадратної матриці називається алгебраїчна сума n! членів (доданків), кожен з яких є добутком n елементів, взятих з різних рядків і з різних стовпчиків, причому цей добуток береться із знаком плюс, якщо перестановка, утворена з других індексів (при умові, що перші йдуть по порядку), парна, і з протилежним знаком, якщо ця перестановка непарна.

Використовуючи вище сказане, пояснимо знаки доданка а₁₃а₂₁а₃₂ та а₁₂а₂₁а₃₃.

Розташуємо перші індекси по порядку, а з других утворимо перестановку 3,1,2 та 2,1,3 відповідно. Перша перестановка є парною, тому знак доданка а₁₃а₂₁а₃₂ плюс, а друга – непарна, тому знак доданка а₁₂а₂₁а₃₃ – мінус.

Властивості детермінанта n-го порядку:

1) Якщо в детермінанті є нульовий рядок, то детермінант дорівнює нулю.

2) Перестановка рядків (стовпчиків) змінює знак детермінанта.

3) Якщо в детермінанті є два однакові рядки, то детермінант дорівнює нулю.

4) Спільний множник k з одного рядка (стовпчика) можна винести за знак детермінанта.

5) Якщо в детермінанті якийсь рядок є сумою двох рядків, то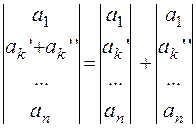

6) Якщо в детермінанті є два пропорційні рядки (стовпчики), то детермінант дорівнює нулю.

7) Якщо в детермінанті k-ий рядок домножити на число р≠0 і додати його до m-го рядка, то детермінант не зміниться.

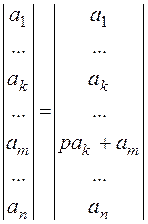
8) Детермінант не змінюється при транспонуванні.

Транспонування – перехід від даного детермінанта до нового, одержаного з даного за таким правилом: всі рядки детермінанта записуються відповідними стовпчиками в новому детермінанті.

9) 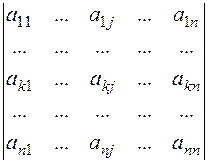=(-1)¹⁺ⁱM_i1a_k1+…+(-1)ⁱ⁺ⁿM_ina_kn = =a_k1A_i1+a_k2A_i2+a_knA_in = 0

Сума добутків елементів рядка на чужі алгебраїчні доповнення дорівнює нулю.

Сума добутків елементів рядка на свої алгебраїчні доповнення дорівнює детермінанту.

Приклад.

1) Розв’язати систему рівнянь методом Крамера:

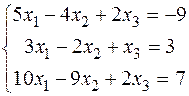
А = 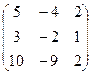В =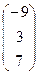

D = 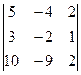= -20-40-54+40+24+45 = -5

D₁ = 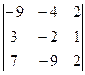= 36-28-54+28-81+24 = -75 х₁ = -75/(-5) = 15

D₂ = 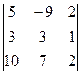= 30-90+42-60+54-35 = -59 x₂ = -59/(-5) = 59/5

D₃ = 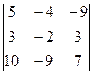= -70+243-120-180+84+135 = 92 x₃ = 92/(-5)= = -92/5

Розв’язок х=(15,59/5,92/5).

2) Розв’язати систему рівнянь методом Крамера:

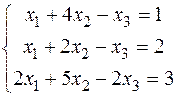
D = 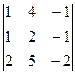= -4-8-5+4+8+5 = 0

D₁ = 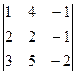= -4-12-10+6+16+5 = 1

D₂ = 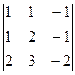= -4-2-3+4+2+3 = 0

D₃ = 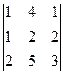= 6+16+5-4-12-10 = 1

Система несумісна.

3) Розв’язати систему рівнянь методом Крамера:

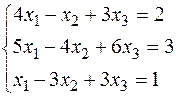
D = 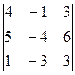= -48-6-45+12+15+72 = 0

D₁ = 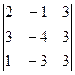= -24-6-27+12+9+36 = 0

D₂ = 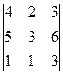= 36+12+15-9-30-24 = 0

D₃ = 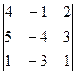= -16-3-30+8+5+36 = 0

Систему методом Крамера розв’язати не можна. Складемо розширену матрицю системи і зведемо її до діагонального виду.

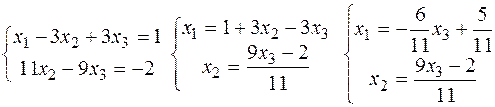
Загальний розв’язок х=(, , 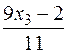x₃), x₃ є R.

Date: 2015-04-23; view: 631; Нарушение авторских прав