Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Алгебраїчне доповнення елемента
|
|
Нехай дана квадратна матриця n-го порядку
A =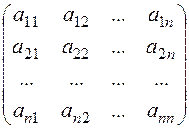 
Означення. Мінором (n-1)-го порядку М квадратної матриці А n-го порядку називається детермінант матриці (n-1)-го порядку, який утворений з матриці А викресленням i-го рядка та j-го стовпчика.
Матриця А n-го порядку має n2 мінорів (n-1)-го порядку.
Означення. Алгебраїчним доповненням елемента аij квадратної матриці А n-го порядку називається мінор Мij матриці А, помножений на (-1)i+j, тобто Аij=(-1)i+jМij
Приклад 1.
Обчислити всі мінори і алгебраїчні доповнення 2-го порядку визначника
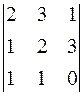
M11 =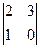 
= -3 M21 = 
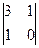= -1 M31 = 
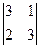= 7
M12 =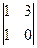 
= -3 M22 = 
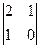=-1 M32 = 
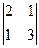= 5
M13 =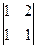 
= -1 M23 = 
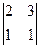= -1 M33 = 
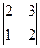= 1
A11 = -3, A12 = 3, A13 = -1,
A21 = 1, A22 = -1, A23 = 1,
A31 = 7, A32 = -5, A33 = 1.
Лема. Детермінант D, в якого всі елементи i-го рядка (або j-го стовпця), крім елемента аij, дорівнюють нулю, дорівнює добутку елемента аij на його алгебраїчне доповнення, тобто D=аijАij.
Теорема. Визначник D=ïаijï n-го порядку дорівнює сумі всіх попарних добутків елементів будь-якого рядка або стовпця на їх алгебраїчні доповнення, тобто
D=аi1Аi1+…+аinАin,
D=а1jА1j+…+аjnАj1
Перша з них – це розклад детермінанта за елементами i-го рядка, друга – розклад детермінанта за елементами j-го стовпця.
Наслідок. Детермінант квадратної матриці n-го порядку дорівнює нулю, якщо всі мінори (n-1)–го порядку дорівнюють нулю.
Теорема. Сума всіх попарних добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) цього визначника дорівнює нулю.
Наслідок. a1jА1m+…+аnjАnm=0 (j¹m)
ai1Ak1+…+ainAkn=0 (i¹k).
Приклад 2.
Обчислити детермінант
1 спосіб. Розкладемо детермінант за елементами першого стовпчика
D=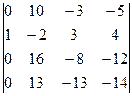 
= 3(-1)2 
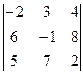+ 1(-1)3 
+
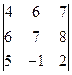+ 5(-1)4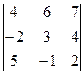 
+ 4(-1)5 
=
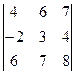=3(-28+120-24-140-36-16)-(56+240-42-245-72+32)+5(24+120+14-
-105+24+16)-4(96+144-98-126+96-112)=-372+31+465=124.
2 спосіб. За допомогою елемента a21 = 1 обнулимо всі інші елементи першого стовпчика і для обчислення використаємо лему
D= 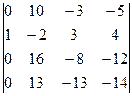= 1(-1)3 
=
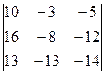= -(1120+468+1040-520--672-1560)=124.
Date: 2015-04-23; view: 587; Нарушение авторских прав