
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Однорідні системи лінійних рівнянь. Фундаментальна система розв’язків однорідної системи
|
|
Лінійне рівняння а1х1+а2х2+…+аnхn=b називається однорідним, якщо його вільний член b дорівнює нулю.
Систему лінійних рівнянь, в якій всі вільні члени дорівнюють нулю, називають однорідною системою лінійних рівнянь (СЛОР).
Загальний вигляд СЛОР:
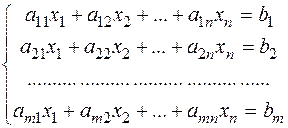 (1)
(1)
Будь-яка однорідна лінійна система сумісна. Вона завжди має розв’язок х=(0,0,…,0)- нульовий (тривіальний) розв’язок. Будь-який розв’язок СЛОР, відмінний від нульового називають ненульовим (нетривіальним) розв’язком. Насправді, не будь-яка СЛОР має ненульові розв’язки.
Теорема. (достатня умова існування ненульових розв’язків СЛОР)
Однорідна система лінійних рівнянь, в якій кількість рівнянь менша кількості невідомих, має ненульові розв’язки.
Розв’язки СЛОР мають такі властивості:
1) Якщо вектор b=(b1,b2,…,bn) є розв’язком системи (1), то при довільному числі k вектор kb=(kb1,kb2,…,kbn) також буде розв’язком цієї системи.
2) Будь-яка лінійна комбінація розв’язків однорідної системи (1) сама буде розв’язком цієї системи.
Розглянемо множину L розв’язків СЛОР. Нехай а=(а1,а2,…,аn) і b=(b1,b2,…,bn) є розв’язками СЛОР. Покажемо, що множина розв’язків СЛОР утворює підпростір Vn, тобто, що виконуються такі умови:
1) a+b=(а1+b1,а2+b2,…,а3+bn);
2) ka=(kа1,kа2,…,kаn).
Вектори a+b i ka є розв’зками СЛОР за властивістю розв’язків СЛОР.
Отже, множина розв’язків СЛОР утворює підпростір Vn.
У випадку неоднорідної системи така властивість місця не має.
Теорема 7. (про розмірність простору розв’язків СЛОР)
Розмірність простору розв’язків СЛОР дорівнює різниці кількості змінних n і рангу основної матриці системи r.
dimL=n-r
Означення. Будь-яка лінійно незалежна система векторів однорідної системи лінійних рівнянь, через яку лінійно виражається довільний розв’язок цієї системи, називається її фундаментальною системою розв’язків.
Іншими словами базис простору розв’язків СЛОР називається фундаментальною системою розв’язків.
Приклад.
1) Побудувати простір розв’язків СЛОР:
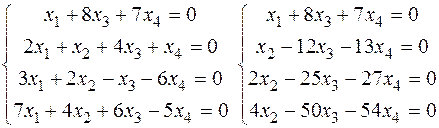
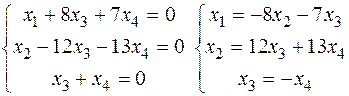
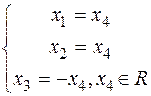
Загальний розв’язок системи х=(х4,х4,-х4,х4),х4 є R.
Знайдемо фундаментальну систему розв’язків ФСР. Для цього вільним змінним надамо довільних значень. Зауважимо, що не можна всім вільним змінним одночасно надавати значення 0, бо нуль-вектор не може належати до базиса простору розв’язків СЛОР. Надамо змінній х4 значення 1, одержимо один вектор ФСР а=(1,1,-1,1).
Знаючи базис простору розв’язків можна записати L={bïb=ka, k є R}.
2) Побудувати простір розв’язків СЛОР:

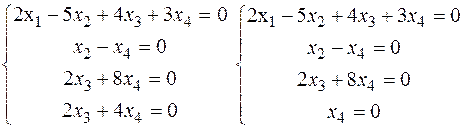
х1=х2=х3=х4=0. Так як розв’язком СЛОР є лише нульовий вектор, то ФСР не існує.
3) Побудувати простір розв’язків СЛОР:
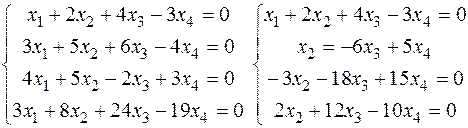

Загальний розв’язок системи (8х3-7х4,-х3+5х4,х3,х4),х3,x4єR.
Для знаходження базису простору складемо табличку
| X1 | X2 | X3 | X4 |
| -6 | |||
| -7 |
Фундаментальна система розв’язків: а1=(8,-6,1,0), а2=(-7,5,0,1).
Знаючи базис простору розв’язків можна записати
L={bïb=k1a1+k2a2, k1,k2 є R}.
Date: 2015-04-23; view: 2211; Нарушение авторских прав