
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Базис і ранг скінченної системи векторів векторного простору
|
|
Нехай а1,а2,…,аm (3) –довільна система векторів простору Vn і аi1,аi2,…,аin (4) –деяка лінійно незалежна підсистема цієї системи.
Означення. Лінійно незалежна підсистема (4) системи векторів (3) називається базисом системи (3), якщо кожний вектор системи (3) є лінійною комбінацією векторів цієї підсистеми.
Теорема 6. Два різних базиса однієї і тієї ж системи векторів містять однакову кількість векторів.
Наприклад за базис V3 можна взяти систему е1=(1,0,0), е2=(0,1,0), е3=(0,0,1) або а1=(1,2,-2), а2=(0,-1,3), а3=(0,-2,4).
Але система b1=(1,-2,-3), b2=(1/2,-1,-3/2), b3=(4,5,6) не є базисом так, як вона містить пропорційні рядки, тобто є лінійно залежною.
Означення. Кількість векторів, які входять в будь-який базис даної системи векторів, називається рангом цієї системи.
Ранг системи векторів – це максимальне число лінійно незалежних векторів системи.
Приклад.
1) Знайти один з базисів системи векторів і виразити всі її вектори, що не входять до знайденого базису, через цей базис:
а1 = (4,1,2), а2 = (1,0,3), а3 = (2,3,-5), а4 = (1,1,6).
Складемо матрицю, рядками якої є дані вектори і зведемо її до діагонального виду
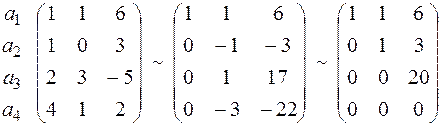
При елементарних перетвореннях координати вектора а перетворилися в 0, тому базисом даної системи векторів є вектори а2,а3,а4.
Виразимо вектор а1 через базис: а1=k1a2+k2a3+k3a4, де ki невідомі коефіцієнти. Складемо матрицю даного рівняння:
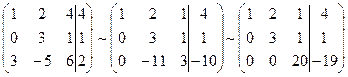
Одержимо систему 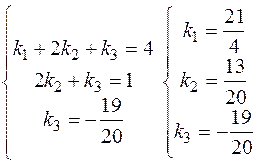
Отже, а1=21/4a2+13/20a3-19/20a4.
Іншим базисом даної системи векторів є вектори а1,а2,а3.
Означення. Системою твірних називається система векторів а1,а2,…,аn множини векторів лінійного простору, якщо будь-який вектор з цієї множини можна лінійно виразити через скінченне число векторів а1,а2,…,аn:
a1,а2,…,аn – система твірних º "аi (аi=k1a1+k2a2+…+knan).
Ознака лінійної залежності системи векторів - cистема векторів лінійно залежна тоді і тільки тоді, коли знайдеться вектор в цій системі, який є лінійною комбінацією інших векторів цієї системи:
a1,а2,…,аn – лінійно залежна ó $ai (ai=k1a1+k2a2+…+knan).
Означення. Лінійно незалежна система твірних називається базисом векторного простору.
Ознака базису: базис – максимально лінійно незалежна система векторів. Максимальна в тому розумінні, що якщо до неї приєднати ще один вектор, то вона стане лінійно залежною.
Теорема. Кількість векторів в довільному базисі скінченно вимірного простору є інваріантом цього простору (одна і та ж для простору), а розмірність простору дорівнює кількості векторів в базисі цього простору.
Наприклад, система з 5 лінійно незалежних векторів утворює базис, а система з 6 векторів є лінійно залежною і базис на утворює.
Date: 2015-04-23; view: 2383; Нарушение авторских прав