Лінійна залежність векторів

Означення. Вектор b з простору Vn називається пропорційним вектору a з цього ж простору, якщо існує таке число k таке, що b=ka.

Нульовий вектор q=(0,0,…,0) пропорційний будь-якому вектору а=(а₁,а₂,…,а_n) тому, що q = 0*а.

Нехай а₁,а₂,…,а_m (1) довільна система векторів з простору.

Означення.Вектор b є Vn називається лінійною комбінацією векторів а₁,а₂,…,а_m, якщо існують такі числа k₁,k₂,…,k_m, що

b=k₁a₁+k₂a₂+…+k_ma_m (2)

Числа k₁,k₂,…,k_n називаються коефіцієнтами цієї лінійної комбінації.

Нульовий вектор q=(0,0,…,0) є лінійною комбінацією векторів будь-якої системи, оскільки q=0*а₁+0*а₂+…+0*а_m.

Означення. Система векторів а₁,а₂,…,а_m простору Vn називається лінійно залежною, якщо існують такі числа k₁,k₂,…,k_m не всі рівні нулю і

k₁a₁ +k₂a₂+…+k_ma_m=0. (*)

Система векторів називається лінійно незалежною, якщо рівність (*) виконується лише при k₁ = k₂ = …= k_m = 0.

Приклади.

1) З’ясувати лінійно залежною чи лінійно незалежною є система векторів

a₁=(1,-2,-3), а₂=(2,3,4), а₃=(3,5,7).

Запишемо рівняння (*) k₁a₁+k₂a₂+k₃a₃=0. Звідси одержимо систему

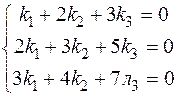
Розв’яжемо її методом Гауса

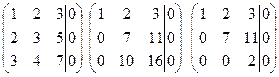
=> x₁=x₂=x₃=0.

Отже, система векторів є лінійно незалежною.

2)а₁ = (1,2sinA,tgA,2cosA)

a₂ = (ctgA,2cosA,1,0)

a₃ = (cosA,sin2A,sinA,1+cos2A),

a₄ = (tgA,1,0,2sinA).

Аналогічно попереднім міркуванням маємо:

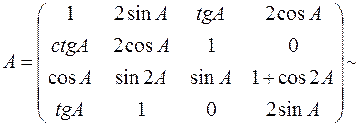
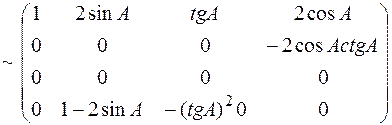
k₄ = 0, k₂ = tgA/2/(1-2sinAtgA)k₃

Отже, існує k₂¹0, а рівняння (*) виконується. Отже, система лінійно залежна.

Теорема 1. (ознака лінійної залежності системи)

Система векторів (1) лінійно залежна тоді і тільки тоді, коли хоча б один з векторів цієї системи є лінійною комбінацією інших її векторів.

Наслідок 1. Будь-яка система векторів, яка містить нульовий вектор, лінійно залежна.

Наслідок 2. Якщо в системі є пропорційні (колінеарні) вектори, то система лінійно залежна.

Теорема 2. Якщо система векторів а₁,а₂,…,а_m лінійно незалежна, а система векторів а₁,а₂,…,а_m,b лінійно залежна, то вектор b є лінійною комбінацією векторів а₁,а₂,…,а_m.

Означення. Множина, яка складається з будь-яких k (k£m) векторів системи (1) називається підсистемою цієї системи.

Теорема 3. Якщо деяка підсистема системи векторів (1) лінійно залежна, то і система (1) лінійно залежна.

Наслідок. Якщо система векторів (1) лінійно незалежна, то і будь-яка її підсистема теж лінійно незалежна.

Теорема 4. Будь-які s векторів арифметичного n-мірного простору складають при s>n лінійно залежну систему.

Date: 2015-04-23; view: 766; Нарушение авторских прав