
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Елементарні перетворення
|
|
Означення. Елементарними перетвореннями системи лінійних рівнянь називаються такі перетворення:
1) перестановка місцями (транспозиція) двох рівнянь системи;
2) множення будь-якого рівняння системи на число, відмінне від нуля;
3) додавання до одного рівняння системи іншого її рівняння, помножене на деяке число;
4) викреслення невизначеного рівняння.
Теорема Гауса. Елементарні перетворення системи не змінюють множину її розв’язків, тобто приводять нас до рівносильної системи.
Ідея метода Гауса СЛР полягає в тому, що за допомогою елементарних перетворень переходимо від даної системи до системи виду трикутника або трапеції і розв’язуємо одержану систему, а оскільки вона рівносильна даній, то одержуємо розв’язок (множину розв’язків) початкової системи.
Алгоритм:
1) якщо в системі є суперечливе рівняння, то система несумісна;
2) якщо в системі є невизначене рівняння, то викреслюємо його;
3) робимо коефіцієнт а11¹0;
4) перше рівняння залишаємо, наступні рівняння утворюємо так:
перше рівняння а11х1+а12х2+…+а1nхn=b1 домножуємо на
–а1n/а11 і додаємо до наступних.
В результаті одержимо систему:
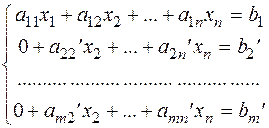
Далі аналогічно беремо рівняння a22¢x2+…+a2n¢xn=b2¢ і обнуляємо коефіцієнти аk2¢, k³3.
Отже, дану систему ми звели до діагонального виду

в якій діагональні елементи аii¹0(i=1,…,r,r<=k).
В результаті цих перетворень, якщо матриця СЛР зводиться:
1) до виду трикутника, то СЛР має єдиний розв’язок;
2) до виду трапеції, тоді СЛР має безліч розв’язків.
Змінні, через які ми виражаємо всі інші змінні називаються вільними змінними.
Для зручності обчислень будемо використовувати матриці, бо перетворення з рядками зводяться до переворень з коефіцієнтами.
Приклад.
1) Розв’язати систему лінійних рівнянь методом Гауса:
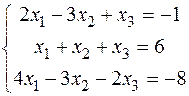
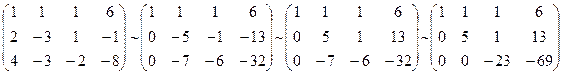
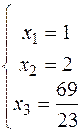
Дана система звелась до виду трикутника. Її розв’язок (1,2,69/23).
2) Розв’язати систему лінійних рівнянь методом Гауса:
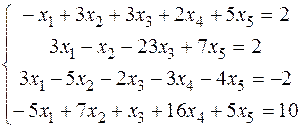
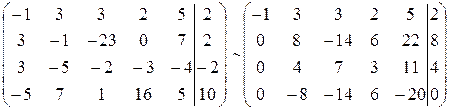 ~
~
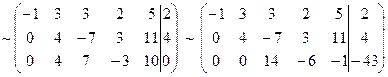
х1=-12-44 3/4x3+26 3/4x4,
x2=-19-39 1/4x3+18 1/4x4,
x3,x4 є R,
x5=4+14x3-6x4.
Cистема звелась до виду трапеції.
Її розв’язок (-12-44 3/4x3+26 3/4x4, -19-39 1/4x3+18 1/4x4, x3,x4,
4+14x3-6x4), х3,x4 є R.
3) Розв’язати систему лінійних рівнянь методом Жордана-Гауса:
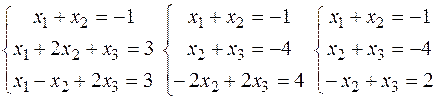
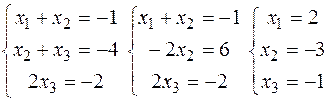
Отже її розв’язок (2,-3,-1).
4) Розв’язати систему лінійних рівнянь:
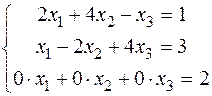
Дана система містить суперечливе рівняння, отже вона розв’язків немає.
Date: 2015-04-23; view: 1228; Нарушение авторских прав