Векторні простори.Арифметичний n-мірний векторний простір

Означення. Множина із введеними на ній алгебраїчними операціями називається алгеброю.

Алгебри класифікують за властивостями операцій.

Означення. Mножина G із введеною на ній алгебраїчною операцією * називається групою, якщо виконуються такі властивості:

1) асоціативність операції "a,b,c є G ((a*b)*c=a*(b*c));

2) нейтральний елемент "a є G $e (a*e=e*a=a);

3) симетричний елемент "a є G $a¢ (a*a¢=a¢*a=e).

Означення. Група називається абелевою, якщо операція комутативна, тобто:

"a "b (a*b=b*a).

Означення. Множина <K,+,* > називається кільцем, якщо:

1) <K,+> - абелева група;

2) * - асоціативна;

3) дистрибутивні закони

"a,"b,"c є K ((a+b)c=ac+bc)

(c(a+b)=ca+cb).

Означення. Кільце називається комутативним, якщо операція множення комутативна.

Означення. Комутативне кільце з одиницею, в якому

"a ≠ 0 $ a^-1 (a*a^-1=1), називається полем.

Приклади алгебр.

1. R–кільце (по додаванню і множенню), Q - комутативне кільце;

2. Z - комутативне кільце (по додаванню і множенню);

3. Z,Q – абелеві групи;

4. R – поле.

Mножина всіх n–мірних числових векторів - абелева група відносно додавання.

Означення. Векторним (лінійним) простором над полем Р називають множину елементів довільної природи, в якій введено операції додавання і множення на елементи поля (скаляри) і виконуються аксіоми:

1) <V,+> - абелева група;

2) Операція множення на скаляр асоціативна

"k,l є P, "a є Vn ((kl)a=k(la));

3) "a є Vn (1*a=a), 1 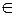P;

4) Операція множення на скаляр дистрибутивна відносно додавання елементів множини Vn

"k є P "a,b є Vn (k(a+b)=ka+kb);

5) Операція множення на скаляр дистрибутивна відносно додавання скалярів "k,l є P "a є V ((k+l)a=ka+kb).

Якщо поле Р - це поле дійсних чисел, то простір Vn називається дійсним векторним (лінійним) простором.

Означення. Множина Vn всіх n-мірних числових векторів з координатами з поля Р з введеними на ній операціями додавання векторів і множення вектора на число з поля Р називається n-мірним арифметичним простором над полем Р.

Приклади векторних просторів:

1) Vn - векторний простір;

2) Множина всіх дійсних функцій, неперервних на відрізку [а,в] - дійсний векторний простір;

3) Поле С комплексних чисел відносно додавання і множення – комплексний векторний простір;

4) Сукупність R[x] всіх многочленів від змінної х з дійсними коефіцієнтами є дійсним лінійним простором;

5) Сукупність матриць n-го порядку над полем Р є лінійним простором над Р відносно додавання і множення на скаляри поля Р(буде показано далі).

Означення. Непорожня підмножина V¢ векторного простору Vn називається підпростором простору, якщо вонa є лінійним простором відносно операцій,

введених у Vn.

Ознака лінійного підпростору – замкненість відносно введеної операції:

V¢–підпростір Vn ó1) "a¢,b¢ є V¢ (a¢+b¢ є V¢);

2) "k є P "a¢ є V¢ (ka¢ є V¢).

Приклади підпросторів:

1) Множина, яка складається лише з нульового елемента є лінійним підпростором будь- якого векторного простору (нульовий підпростір);

2) Векторний простір є своїм підпростором;

3) В арифметичному просторі Vn множина V 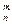(m<n) всіх векторів виду (а₁,а₂,…,а_n,0,...,0) є лінійним підпростором;

4) Простір розв’язків системи лінійних однорідних рівнянь є підпростором (буде показано далі).

Date: 2015-04-23; view: 1009; Нарушение авторских прав