Вектори. Дії над векторами

Міністерство освіти і науки України

Черкаський національний університет

Імені Богдана Хмельницького

Ілляшенко Н.Г.

Лінійна алгебра

Частина I

Навчально – методичний посібник для організації
самостійної роботи студентів

Черкаси

Посібник містить теоретичні відомості курсу теорії многочленів. Кожен розділ посібника супроводжується набором прикладів розв’язування типових задач.

Посібник призначений для організації самостійної роботи студентів стаціонарної та заочної форм навчання.

Рецензент: Атамась В.В. – кандидат фіз-мат наук, доцент кафедри алгебри, геометрії та МВМ ЧНУ

ім. Б. Хмельницького.

Розділ 1. Векторні простори та системи лінійних рівнянь.

Вектори. Дії над векторами.

Для побудови загальної теорії систем лінійних рівнянь введемо поняття n-мірного числового вектора та простору дійсних чисел. З шкільного курсу математики відомо, що довільний вектор площини можна записати а=k₁e₁+k₂e₂, де k₁,k₂ - елементи поля дійсних чисел, а е₁,е₂ – орти, або їх називають базисом двоxвимірного простору. Якщо в множині векторів звичайного простору вибрати деякий базис e₁,e₂,e₃, то будь-який вектор a можна розкласти по векторам e₁,e₂,e₃:

a=a₁e₁+a₂e₂+a₃e₃,

причому коефіцієнти a₁,a₂,a₃ в розкладі визначаються єдиним чином. Їх називають координатами вектора a в базисі e₁,e₂,e₃. Дану рівність можна записати так: a=(a₁,a₂,a₃)

Нехай a=(a₁,a₂,a₃), b=(b₁,b₂,b₃) і k - деяке число, то

1) a=b ó a₁=b₁ Ù a₂=b₂ Ù a₃ =b₃;

2) ka=(ka₁,ka₂,ka₃);

3) a+b=(a₁+b₁,a₂+b₂,a₃+b₃).

Означення. Будь-яка впорядкована система n чисел a₁,a₂,…,a_n з поля P (деяке числове поле) називається n-мірним числовим вектором; числа a₁,a₂,…,a_n називаються його координатами або компонентами:

a₁–першою координатою, a₂–другою координатою,…, a_n–n-ою.

Числові вектори будемо позначати a,b,c,….

Координати а_1, a_2,…,a_n n-мірного числового вектора а розташовують в рядок або стовпчик:

1) a=(a₁,a₂,…,a_n); 2) a=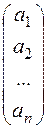

Означення. Числові вектори a=(a₁,a₂,…,a_n), b=(b₁,b₂,…,b_n) рівні тоді і тільки тоді, коли рівні їх відповідні координати, тобто

a=b ó a₁=b₁ Ù a₂=b₂ Ù … Ù a_n=b_n.

Означення. Сумою a+b векторів a=(a₁,a₂,…,a_n), b=(b₁,b₂,…,b_n) називається вектор c=(a₁+b₁,a₂+b₂,…,a_n+b_n).

Означення. Добутком вектора a=(a₁,a₂,…,a_n) на число k є P називається вектор ka=(ka₁,ka₂,…,ka_n).

Нульовий вектор q=(0,0,…,0).

Date: 2015-04-23; view: 888; Нарушение авторских прав